题目内容
(文)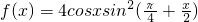 +
+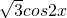 -2cosx.
-2cosx.
(1)求f(x)的周期;
(2)若B为△ABC的内角且f(B)=2,求角B;
(3)若B为△ABC的内角且f(B)-m>2恒成立,求实数m取值范围.
解:(1)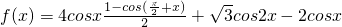
=2cosx(1+sinx)+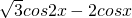 =
=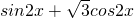 =
=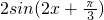 .
. .
.
(2)∵f(B)=2,∴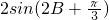 =2,
=2,
∴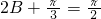 ,∴B=
,∴B=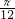 .
.
(3)f(B)-m>2恒成立,即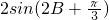 >2+m恒成立,
>2+m恒成立,
∵0<B<π,
∴-2≤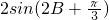 ≤2,∴2+m<-2,∴m<-4.
≤2,∴2+m<-2,∴m<-4.
分析:(1)欲求f(x)的周期,须将函数f(x)化成一个角的一个三角函数的形式才好求解,故先利用三角函数的和角公式、二倍角公式将原函数化成一个三角函数的形式,最后利用周期公式即可求解;
(2)利用(1)中化得的f(x)的形式,由f(B)=2得到一个关于角B的方程,解此三角方程即可求得角B;
(3)利用三角函数的有界性,最终转化为2+m小于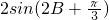 的最小值即可,从而求出实数m取值范围.
的最小值即可,从而求出实数m取值范围.
点评:本题主要考查了函数恒成立问题、同角三角函数基本关系的运用、三角函数的周期性及其求法等知识.属于基础题.
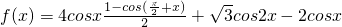
=2cosx(1+sinx)+
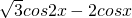 =
=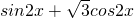 =
=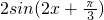 .
. .
.(2)∵f(B)=2,∴
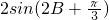 =2,
=2,∴
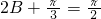 ,∴B=
,∴B=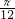 .
.(3)f(B)-m>2恒成立,即
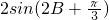 >2+m恒成立,
>2+m恒成立,∵0<B<π,
∴-2≤
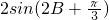 ≤2,∴2+m<-2,∴m<-4.
≤2,∴2+m<-2,∴m<-4.分析:(1)欲求f(x)的周期,须将函数f(x)化成一个角的一个三角函数的形式才好求解,故先利用三角函数的和角公式、二倍角公式将原函数化成一个三角函数的形式,最后利用周期公式即可求解;
(2)利用(1)中化得的f(x)的形式,由f(B)=2得到一个关于角B的方程,解此三角方程即可求得角B;
(3)利用三角函数的有界性,最终转化为2+m小于
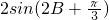 的最小值即可,从而求出实数m取值范围.
的最小值即可,从而求出实数m取值范围.点评:本题主要考查了函数恒成立问题、同角三角函数基本关系的运用、三角函数的周期性及其求法等知识.属于基础题.

练习册系列答案
相关题目
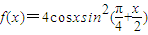 +
+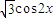 -2cosx.
-2cosx.