题目内容
已知函数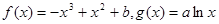 .
.
(Ⅰ)若 在
在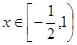 上的最大值为
上的最大值为 ,求实数
,求实数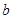 的值;
的值;
(Ⅱ)若对任意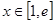 ,都有
,都有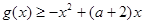 恒成立,求实数
恒成立,求实数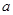 的取值范围;
的取值范围;
(Ⅲ)在(Ⅰ)的条件下,设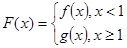 ,对任意给定的正实数
,对任意给定的正实数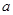 ,曲线
,曲线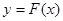 上是否存在两点
上是否存在两点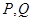 ,使得
,使得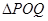 是以
是以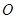 (
(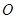 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在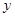 轴上?请说明理由.
轴上?请说明理由.
【答案】
(Ⅰ) .(Ⅱ)
.(Ⅱ) .
.
(Ⅲ)对任意给定的正实数 ,曲线
,曲线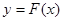 上总存在两点
上总存在两点 ,
, ,使得
,使得 是以
是以 (
( 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在 轴上.
轴上.
【解析】
试题分析:(Ⅰ)由 ,得
,得 ,
,
令 ,得
,得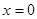 或
或 .
.
当 变化时,
变化时,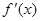 及
及 的变化如下表:
的变化如下表:
|
|
|
|
|
|
|
|
|
|
|
- |
|
+ |
|
- |
|
|
|
↘ |
极小值 |
↗ |
极大值 |
↘ |
由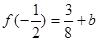 ,
,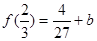 ,
,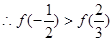 ,
,
即最大值为 ,
, .
4分
.
4分
(Ⅱ)由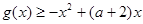 ,得
,得 .
.
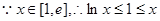 ,且等号不能同时取,
,且等号不能同时取,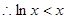 ,即
,即
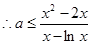 恒成立,即
恒成立,即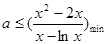 .
6分
.
6分
令 ,求导得,
,求导得, ,
,
当 时,
时,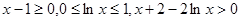 ,从而
,从而 ,
,
 在
在 上为增函数,
上为增函数,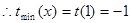 ,
, .
8分
.
8分
(Ⅲ)由条件,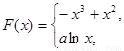
 ,
,
假设曲线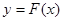 上存在两点
上存在两点 ,
, 满足题意,则
满足题意,则 ,
, 只能在
只能在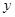 轴两侧,
轴两侧,
不妨设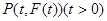 ,则
,则 ,且
,且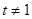 .
.
 是以
是以 为直角顶点的直角三角形,
为直角顶点的直角三角形, ,
,

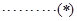 ,
,
是否存在 ,
, 等价于方程
等价于方程 在
在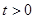 且
且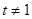 时是否有解.
10分
时是否有解.
10分
①若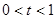 时,方程
时,方程 为
为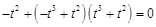 ,化简得
,化简得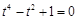 ,此方程无解;
,此方程无解;
②若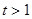 时,方程
时,方程 为
为 ,即
,即 ,
,
设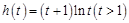 ,则
,则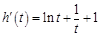 ,
,
显然,当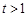 时,
时,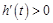 ,
,
即 在
在 上为增函数,
上为增函数,
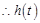 的值域为
的值域为 ,即
,即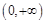 ,
,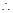 当
当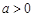 时,方程
时,方程 总有解.
总有解.
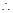 对任意给定的正实数
对任意给定的正实数 ,曲线
,曲线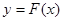 上总存在两点
上总存在两点 ,
, ,使得
,使得 是以
是以 (
( 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在 轴上. 14分
轴上. 14分
考点:利用导数研究函数的单调性、最值。
点评:难题,在给定区间,导数非负,函数为增函数,导数非正,函数为减函数。涉及“不等式恒成立”问题,往往通过构造函数,转化成求函数的最值问题,利用导数加以解决。本题(III)需要分类讨论,易于出错,是叫男的一道题目。

练习册系列答案
相关题目







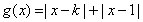
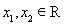
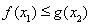
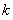
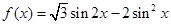 .
.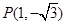 在角
在角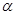 的终边上,求
的终边上,求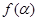 的值;(Ⅱ)若
的值;(Ⅱ)若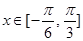 ,求
,求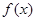 的值域.
的值域.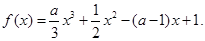
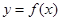 在点
在点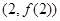 处的切线与直线
处的切线与直线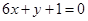 平行,求出这条切线的方程;
平行,求出这条切线的方程;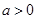 ,讨论函数
,讨论函数 的单调区间;
的单调区间;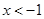 ,恒有
,恒有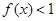 ,求实数
,求实数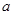 的取值范围.
的取值范围.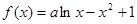 .
.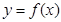 在
在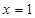 处的切线方程为
处的切线方程为 ,求实数
,求实数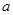 和
和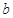 的值;
的值;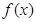 的单调性;
的单调性; 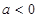 ,且对任意
,且对任意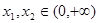 ,都有
,都有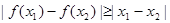 ,求
,求