题目内容
已知函数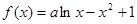 .
.
(Ⅰ)若曲线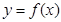 在
在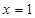 处的切线方程为
处的切线方程为 ,求实数
,求实数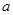 和
和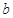 的值;
的值;
(Ⅱ)讨论函数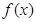 的单调性;
的单调性;
(Ⅲ)若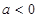 ,且对任意
,且对任意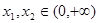 ,都有
,都有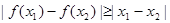 ,求
,求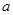 的取值范围.
的取值范围.
【答案】
(1) 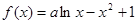 求导得
求导得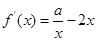 在
在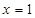 处的切线方程为
处的切线方程为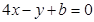 ,
, ,得
,得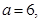
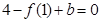 ;b=-4.
;b=-4.
(2) 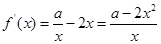
当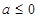 时,
时,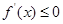 在
在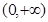 恒成立,所以
恒成立,所以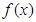 在
在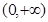 上是减函数,
上是减函数,
当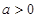 时,
时,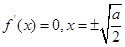 (舍负)
(舍负)
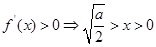 ,
,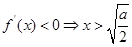
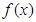 在
在 上是增函数,在
上是增函数,在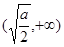 上是减函数;
上是减函数;
(3) 若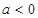 ,
,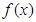 在
在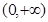 上是减函数,
上是减函数,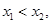 ,
,
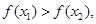
 即
即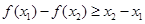
即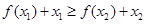 ,只要满足
,只要满足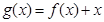 在
在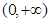 为减函数,
为减函数,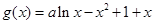 ,
,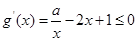 即
即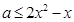 在
在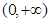 恒成立,
恒成立, ,
,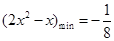 ,所以
,所以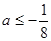
【解析】(1)根据切线的斜率求a,然后求b;(2)讨论a的正负;(3) 转化为
转化为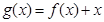 在
在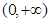 为减函数来解决。
为减函数来解决。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ,
,
 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求
在它们的交点(1,c)处具有公共切线,求 ,
,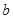 的值;
的值; ,
, 时,若函数
时,若函数 在区间[
在区间[ ,2]上的最大值为28,求
,2]上的最大值为28,求 ,
, 在
在 上的最大值为
上的最大值为 ,求实数
,求实数 的值;
的值; ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,对任意给定的正实数
,对任意给定的正实数 上是否存在两点
上是否存在两点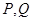 ,使得
,使得 是以
是以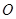 (
( 轴上?请说明理由。
轴上?请说明理由。