题目内容
2.试求函数f(x)=x(2-|x|)在x=0处的导数值f′(0)分析 求出函数在x=0处的左导数和右导数,即可得到结论.
解答 解:当x>0时,f(x)=x(2-x)=2x-x2,导数f′(x)=2-2x,
当x<0时,f(x)=x(2+x)=2x+x2,f′(x)=2+2x,
则函数的右导数f′+(0)=2,
函数的左导数f′-(0)=2,
∵f′+(0)=f′-(0)=2,
∴f′(0)=2.
点评 本题主要考查函数导数的计算,根据导数的定义,计算函数在x=0处的左导数和右导数是解决本题的关键.

练习册系列答案
相关题目
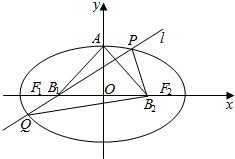 如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为1的直角三角形.
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为1的直角三角形.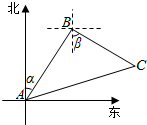 如图所示,一架飞机从A地沿北偏东35°的方向飞行800km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800km送往C地医院,求这架飞机飞行的路程及两次位移的和.
如图所示,一架飞机从A地沿北偏东35°的方向飞行800km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800km送往C地医院,求这架飞机飞行的路程及两次位移的和. 分别为正方形
分别为正方形 的边
的边 和
和 的中点,则
的中点,则 ( )
( ) B.
B. C.
C. D.
D.
 为单位向量,其夹角为60°,则
为单位向量,其夹角为60°,则 _________.
_________. ,
, 是线段
是线段 上异于
上异于 的一点,
的一点, ,
, 均为等边三角形,则
均为等边三角形,则 的外接圆的半径的最小值是 .
的外接圆的半径的最小值是 .