题目内容
12.比较各数:2${\;}^{\frac{2}{3}}$,($\frac{3}{4}$)${\;}^{\frac{1}{3}}$,1,($\frac{4}{3}$)${\;}^{\frac{2}{3}}$的大小.分析 根据幂函数y=${x}^{\frac{2}{3}}$的图象与性质判断${2}^{\frac{2}{3}}$>${(\frac{4}{3})}^{\frac{2}{3}}$,再根据指数函数的图象与性质判断${(\frac{4}{3})}^{\frac{2}{3}}$>1,${(\frac{3}{4})}^{\frac{1}{3}}$<1;
由此比较题目中各数的大小.
解答 解:∵幂函数y=${x}^{\frac{2}{3}}$在(0,+∞)上是单调增函数,且2>$\frac{4}{3}$,
∴${2}^{\frac{2}{3}}$>${(\frac{4}{3})}^{\frac{2}{3}}$;
又根据指数函数的图象与性质得${(\frac{4}{3})}^{\frac{2}{3}}$>1,${(\frac{3}{4})}^{\frac{1}{3}}$<1;
∴2${\;}^{\frac{2}{3}}$>${(\frac{4}{3})}^{\frac{2}{3}}$>1>($\frac{3}{4}$)${\;}^{\frac{1}{3}}$.
点评 本题考查了利用函数的图象与性质比较大小的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.设函数f(x)是定义在R上的函数,则“x0是函数f(x)的极值点”是“f′(x0)=0”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
7.函数f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
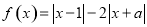 .
.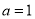 时,求不等式
时,求不等式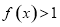 的解集;
的解集;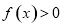 ,在
,在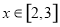 上恒成立,求
上恒成立,求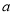 的取值范围.
的取值范围.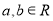 ,则“
,则“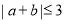 ”是“
”是“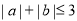 ”的( )
”的( )