题目内容
已知数列 计算
计算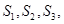 由此推测出
由此推测出 的计算公式,并用数学归纳法证明.
的计算公式,并用数学归纳法证明.
 计算
计算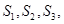 由此推测出
由此推测出 的计算公式,并用数学归纳法证明.
的计算公式,并用数学归纳法证明.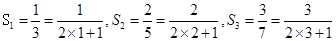 ,推测
,推测 ,证明过程详见解析.
,证明过程详见解析.试题分析:计算
 的值可以推出
的值可以推出 ,利用数学归纳法可以证明,首先验证n=1时,结论成立,接下来假设n=k(
,利用数学归纳法可以证明,首先验证n=1时,结论成立,接下来假设n=k( )时结论成立,即有
)时结论成立,即有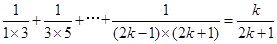 ,最后只需证明n=k+1时,结论也成立,利用
,最后只需证明n=k+1时,结论也成立,利用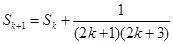 即可得证.
即可得证.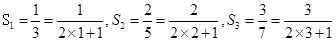 ,
,∴推测
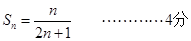
①n=1时,左边=
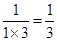 ,右边=
,右边= 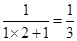 ,左边=右边,所以等式成立 6分
,左边=右边,所以等式成立 6分②假设n=k时等式成立,即有
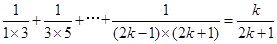 ,
,则当n=k+1时,
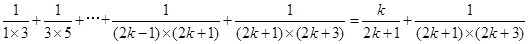

所以当n=k+1时,等式也成立 13分
由①,②可知,对一切
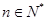 等式都成立 14分.
等式都成立 14分.
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 成立.
成立.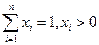 ,求证:
,求证: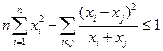 。
。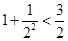
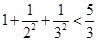
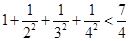

 的第二步中,当
的第二步中,当 时等式左边与
时等式左边与 时的等式左边的差等于 .
时的等式左边的差等于 .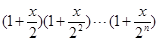 的展开式中,
的展开式中,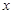 的系数为
的系数为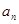 ,
,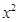 的系数为
的系数为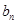 ,其中
,其中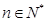
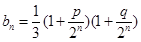 ,对
,对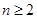 恒成立?证明你的结论.
恒成立?证明你的结论.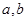 使得关于n的等式
使得关于n的等式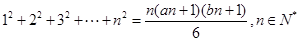
 ;
;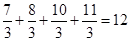 ;
; ;……
;…… 且
且 时,
时, .(最后结果用
.(最后结果用 表示)
表示)