题目内容
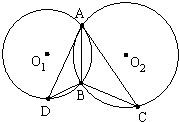如图，⊙O1、⊙O2相交于点A、B，⊙O1的切线AC交⊙O2于另一点C，⊙O2的切线AD交⊙O1于另一点D，求证：AB2=BC•BD
分析：由AC为⊙O1的切线，DA为⊙O2的切线，由弦切角定理，我们可以得到△ABC与△DAB中有两组角对应相等，进而得到两个三角形，△ABC与△DAB相似，根据相似三角形相似的性质得到对应线段成比例，进而得到结论
解答：证明：由条件知∠C=∠DAB，∠CAB=∠D（4分）
∴△ABC∽△DAB（6分）
∴
=
（8分）
∴AB2=BC•BD（10分）
∴△ABC∽△DAB（6分）
∴
| BC |
| AB |
| AB |
| BD |
∴AB2=BC•BD（10分）
点评：本题考查的知识点是相似三角形的判定与性质，弦切角定理，根据要求证的积等式中各线段所在位置，寻找可能相似的三角形并进行证明是解答的关键．
练习册系列答案
相关题目
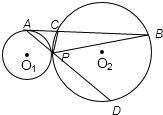
15、如图，⊙O1与⊙O2交于M、N两点，直线AE与这两个圆及MN依次交于A、B、C、D、E；且AD=19，BE=16，BC=4，则AE=
如图，⊙O1和⊙O2公切线AD和BC相交于点D，A、B、C为切点，直线DO1与⊙O1与E、G两点，直线DO2交⊙O2与F、H两点．
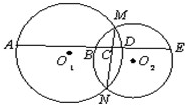选修4-1：几何证明选讲
（选修4-1：几何证明选讲）