题目内容

已知：如图，O1与O2外切于点P，经过O1上一点A作O1的切线交O2于B、C两点，直线AP交O2于点D，连接DC、PC．
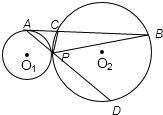
求证：DC2=DP•DA．精英家教网
分析：相切两圆常作的辅助线是：两圆的公切线，因此过点P作两圆的内公切线EP交AB于点F，然后证得△CDP∽△ADC，可得证．
解答：证明：过点P作两圆的内公切线EP交AB于点F，
∵FE、CA都与圆O1相切，精英家教网
∴EP=FA，
∴∠FAP=∠FPA；
∵∠FPA=∠EPA=∠DCP，
∴∠FAP=∠DCP；
∵∠PDC=∠CDA，
∴△CDP∽△ADC；
∴
CD
AD
=
DP
CD
；
∴DC2=DP•DA．
点评：将圆的有关知识与三角形相似结合考查，有一定难度；命题立意：此题主要考查相切两圆的位置关系及弦切角定理，三角形相似的判定等知识．
练习册系列答案
相关题目
选做题（请考生在以下三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）
（1）（不等式选讲）已知函数f（x）=log2（|x-1|+|x-5|-a），当函数f（x）的定义域为R时，则实数a的取值范围为
（-∞，4）
（-∞，4）

（2）（几何证明选讲）如图，AB是半圆O的直径，点C在半圆上，CD⊥AB，垂足为D，且AD=5DB，设∠COD=θ，则tanθ的值为
5
2
5
2
．

（3）（坐标系与参数方程）圆O1和圆O2的极坐标方程分别为ρ=4cosθ，ρ=-4sinθ，则经过两圆圆心的直线的直角坐标方程为
y=x+2
y=x+2
．
（2012•徐州模拟）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，
若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，半径分别为R，r（R＞r＞0）的两圆⊙O，⊙O1内切于点T，P是外圆⊙O上任意一点，连PT交⊙O1于点M，PN与内圆⊙O1相切，切点为N．求证：PN：PM为定值．
B．选修4-2：矩阵与变换
已知矩阵M=
21
34

（1）求矩阵M的逆矩阵；
（2）求矩阵M的特征值及特征向量；
C．选修4-2：矩阵与变换
在平面直角坐标系x0y中，求圆C的参数方程为
x=-1+rcosθ
y=rsinθ
(θ为参数r＞0），以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ+
π
4
)=2
2
．若直线l与圆C相切，求r的值．
D．选修4-5：不等式选讲
已知实数a，b，c满足a＞b＞c，且a+b+c=1，a2+b2+c2=1，求证：1＜a+b＜
4
3
．
已知正三棱柱ABC-A1B1C1，底面边长AB=2，AB1⊥BC1，点O、O1分别是边AC，A1C1的中点，建立如图所示的空间直角坐标系．
（1）求正三棱柱的侧棱长；
（2）若M为BC1的中点，试用基向量
AA1
、
AB
、
AC
表示向量
AM
；
（3）求异面直线AM与BC所成角．
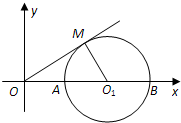精英家教网如图，已知半径为1的⊙O1与x轴交于A，B两点，OM为⊙O1的切线，切点为M，且M在第一象限，圆心O1的坐标为（2，0），二次函数y=-x2+bx+c的图象经过A，B两点．
（1）求二次函数的解析式；
（2）求切线OM的函数解析式；
（3）线段OM上是否存在一点P，使得以P，O，A为顶点的三角形与△OO1M相似．若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

已知正三棱柱ABC—A1B1C1，底面边长AB=2，AB1⊥BC1，点O、O1分别是边AC，A1C1的中点，建立如图所示的空间直角坐标系.

⑴求正三棱柱的侧棱长.

⑵若M为BC1的中点，试用基向量、、表示向量；

⑶求异面直线AB1与BC所成角的余弦值．

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网