题目内容
15、如图，⊙O1与⊙O2交于M、N两点，直线AE与这两个圆及MN依次交于A、B、C、D、E；且AD=19，BE=16，BC=4，则AE=28
．分析：利用相交弦定理推出AB•CD=BC•DE．设CD=x，表示出AB、DE然后解出x，再求出AE．
解答：解：因为A，M，D，N四点共圆，所以AC•CD=MC•CN．同理，有BC•CE=MC•CN．
所以AC•CD=BC•CE，即（AB+BC）•CD=BC•（CD+CE），
所以AB•CD=BC•DE．
设CD=x，则AB=AD-BC-CD=19-4-x=15-x，DE=BE-BC-CD=16-4-x=12-x，
则（15-x）x=4（12-x），即x2-19x+48=0，解得x=3或x=16（舍）．
AE=AB+DE-BD=19+16-7=28．
故答案为：28
所以AC•CD=BC•CE，即（AB+BC）•CD=BC•（CD+CE），
所以AB•CD=BC•DE．
设CD=x，则AB=AD-BC-CD=19-4-x=15-x，DE=BE-BC-CD=16-4-x=12-x，
则（15-x）x=4（12-x），即x2-19x+48=0，解得x=3或x=16（舍）．
AE=AB+DE-BD=19+16-7=28．
故答案为：28
点评：本题主要考查两圆的位置关系，以及相交弦定理的有关知识，分析问题和解决问题的能力，以及转化与化归的思想方法．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
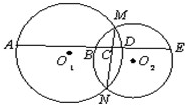选修41：几何证明选讲
选修4-1：几何证明选讲
（选修4-1：几何证明选讲）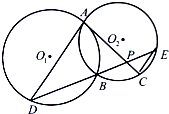
如图，⊙O1与⊙O2相交于A、B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1、⊙O2于点D、E，DE与AC相交于点P．