题目内容
3.有两枚正四面体骰子,各个面分别标有数字1,2,3,4,若同时抛掷两枚骰子,则两枚骰子底面2个数之差的绝对值为2的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 基本事件总数n=4×4=16,用列举法求出两枚骰子底面2个数之差的绝对值为2包含的基本事件的个数,由此能求出两枚骰子底面2个数之差的绝对值为2的概率.
解答 解:有两枚正四面体骰子,各个面分别标有数字1,2,3,4,
同时抛掷两枚骰子,
基本事件总数n=4×4=16,
两枚骰子底面2个数之差的绝对值为2包含的基本事件有:
(1,3),(3,1),(2,4),(4,2),
共有4个,
∴两枚骰子底面2个数之差的绝对值为2的概率是p=$\frac{4}{16}=\frac{1}{4}$.
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
13.$|{\frac{1-2i}{2+i}}|$=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | -i | D. | 2 |
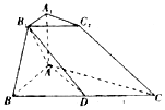 如图所示的三棱台ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,AA1=1,AB=2,BC=4,∠ABB1=45°.
如图所示的三棱台ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,AA1=1,AB=2,BC=4,∠ABB1=45°.