题目内容
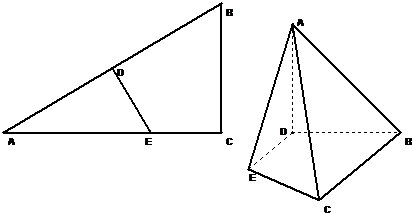 (2013•广东模拟)在△ABC中,∠ACB=90°,∠BAC=30°,AB=4,D、E分别为AB、AC上的点,AB⊥DE,沿DE将△ADE折起,使得平面ADE⊥平面BDEC,设AD=x.
(2013•广东模拟)在△ABC中,∠ACB=90°,∠BAC=30°,AB=4,D、E分别为AB、AC上的点,AB⊥DE,沿DE将△ADE折起,使得平面ADE⊥平面BDEC,设AD=x.(1)试将四棱锥A-BCED的体积u(x)用x表示出来.
(2)当x为何值时,u(x)取最大值.
(3)当u(x)取最大值时,求二面角A-CE-B的某一个三角函数值.
分析:(1)由Rt△ADE∽Rt△ACB得
=
,结合题中数据算出DE=
x,从而得到S△ADE=
x2,结合S△ABC=2
算出S四边形DECB=2
-
x2,由面面垂直的性质定理证出AD⊥平面BDEC,得AD是四棱锥A-BCED的高,再用锥体的体积公式,即可得到四棱锥A-BCED的体积u(x)的表达式;
(2)根据(1)中所得的u(x)的表达式,求导数得u′(x)=
(4-x2).研究u'(x)的正负,可得u(x)的增区间是(0,2),减区间是(2,3),从而得到u(x)最大值为u(2)=
;
(3)过点D作DF⊥CE,交CE的延长线于F,连接AF.根据AD⊥平面BCDE利用三垂线定理,得AF⊥CE,所以∠AFD就是二面角A-CE-B的平面角.Rt△AFD中,算出DF=DEsin60°=
AD×
=1,从而得到tan∠AFD=
=2,即得二面角A-CE-B的正切值等于2.
| AD |
| AC |
| DE |
| BC |
| ||
| 3 |
| ||
| 6 |
| 3 |
| 3 |
| ||
| 6 |
(2)根据(1)中所得的u(x)的表达式,求导数得u′(x)=
3
| ||
| 18 |
8
| ||
| 9 |
(3)过点D作DF⊥CE,交CE的延长线于F,连接AF.根据AD⊥平面BCDE利用三垂线定理,得AF⊥CE,所以∠AFD就是二面角A-CE-B的平面角.Rt△AFD中,算出DF=DEsin60°=
| ||
| 3 |
| ||
| 2 |
| AD |
| DF |
解答:解:(1)根据题意,得Rt△ADE∽Rt△ACB,
∴
=
,结合Rt△ACB中,AC=4cos30°=2
,BC=4sin30°=2
代入得
=
,解得DE=
x,
由此可得S△ADE=
×AD×DE=
x2,而S△ABC=
×AC×BC=
ABcos30°×ABsin30°=2
∴S四边形DECB=S△ABC-S△ADE=2
-
x2
∵平面ADE⊥平面BDEC,平面ADE∩平面BDEC=DE,AD?平面ADE且AD⊥DE
∴AD⊥平面BDEC,AD是四棱锥A-BCED的高线,
因此四棱锥A-BCED的体积V=
SDECB×AD=
(12x-x3),(0<x<3)
即u(x)=
(12x-x3),(0<x<3)
(2)由(1)得u′(x)=
(4-x2),(0<x<3),
令u′(x)>0,得x∈(0,2);令u′(x)<0,得x∈(2,3)
∴u(x)的增区间是(0,2),减区间是(2,3),因此函数u(x)的最大值umax=u(2)=
;
(3)由(2)得当u(x)取最大值时,AD=x=2
过点D作DF⊥CE,交CE的延长线于F,连接AF
∵AD⊥平面BCDE,可得DF是AF在平面BCDE内的射影
∴由三垂线定理,可得AF⊥CE,
因此,∠AFD就是二面角A-CE-B的平面角
∵△DEF中,∠DEF=90°-30°=60°,DE=
AD=
∴DF=DEsin60°=
×
=1
由此可得Rt△AFD中,tan∠AFD=
=2
即二面角A-CE-B的正切值等于2.
∴
| AD |
| AC |
| DE |
| BC |
| 3 |
代入得
| x | ||
2
|
| DE |
| 2 |
| ||
| 3 |
由此可得S△ADE=
| 1 |
| 2 |
| ||
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴S四边形DECB=S△ABC-S△ADE=2
| 3 |
| ||
| 6 |
∵平面ADE⊥平面BDEC,平面ADE∩平面BDEC=DE,AD?平面ADE且AD⊥DE
∴AD⊥平面BDEC,AD是四棱锥A-BCED的高线,
因此四棱锥A-BCED的体积V=
| 1 |
| 3 |
| ||
| 18 |
即u(x)=
| ||
| 18 |
(2)由(1)得u′(x)=
3
| ||
| 18 |
令u′(x)>0,得x∈(0,2);令u′(x)<0,得x∈(2,3)
∴u(x)的增区间是(0,2),减区间是(2,3),因此函数u(x)的最大值umax=u(2)=
8
| ||
| 9 |
(3)由(2)得当u(x)取最大值时,AD=x=2

过点D作DF⊥CE,交CE的延长线于F,连接AF
∵AD⊥平面BCDE,可得DF是AF在平面BCDE内的射影
∴由三垂线定理,可得AF⊥CE,
因此,∠AFD就是二面角A-CE-B的平面角
∵△DEF中,∠DEF=90°-30°=60°,DE=
| ||
| 3 |
2
| ||
| 3 |
∴DF=DEsin60°=
2
| ||
| 3 |
| ||
| 2 |
由此可得Rt△AFD中,tan∠AFD=
| AD |
| DF |
即二面角A-CE-B的正切值等于2.
点评:本题给出平面图形的折叠问题,求四棱锥A-BCED的体积的最大值,并求此时二面角A-CE-B的一个三角函数值,着重考查了解直角三角形、相似三角形、面面垂直的性质定理、锥体的体积公式和利用导数研究函数的单调性等知识,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
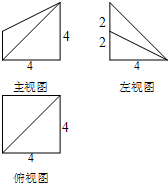 (2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为
(2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为