题目内容
(12分)已知AB是椭圆
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
. (1)设双曲线E2的离心率为
,求关于
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
(1) 
(2) 
解析:
(1)椭圆的右准线:
. 
即
又AB方程:
，
，
，∴
即
∴椭圆的离心率
.从而
(2)由题设
即
.∴
. 解之:
或
.若时,由M(2,1)在椭圆内,矛盾.∴.从而椭圆方程为:为所求.
练习册系列答案
相关题目
上一点，F1，F2是椭圆的两焦点，且满足
（I）求椭圆的两焦点坐标； （II）设点B是椭圆上任意一点，如果|AB|最大时，求证A、B两点关于原点O不对称；
，E、F分别是线段AB、BC的中点，
面ABCD. （1）
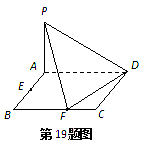证明：PF⊥FD；
分别是椭圆
的左右焦点，其左准线与
轴相交于点N，并且满足
，设A、B是上半椭圆上满足
的两点，其中
.（1）求此椭圆的方程；（2）求直线AB的斜率的取值范围.
是椭圆上纵坐标不为零的两点，若
其中F为椭圆的左焦点．
，焦点在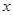
轴上，椭圆的短轴端点和焦点所组成的四边形为正方形，短轴长为2．
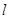过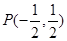
且与椭圆相交于A，B两点，当P是AB的中点时，求直线