题目内容
设a>1,若函数f(x)=loga(ax2-x)在区间[ ,4]上是增函数,则a的取值范围是________.
,4]上是增函数,则a的取值范围是________.
(2,+∞)
分析:设a>1,可得外层函数是增函数,由此知内层函数在[ ,4]也是增函数,由二次函数的性质可以得到关于参数的不等式,再由真数非负,即可求得参数的范围
,4]也是增函数,由二次函数的性质可以得到关于参数的不等式,再由真数非负,即可求得参数的范围
解答:∵a>1
∴f(x)=logax是增函数
又函数f(x)=loga(ax2-x)在区间[ ,4]上是增函数
,4]上是增函数
∴ax2-x在区间[ ,4]上是增函数,且当x=
,4]上是增函数,且当x= 时函数值为正
时函数值为正
∴ 解得a>2
解得a>2
故答案为(2,+∞)
点评:本题考查对数函数的单调性与特殊点,解本题的关键是根据复合函数的单调性判断出内层函数的单调性,由二次的性质得出参数的不等式,解出参数的范围,本题有一易错点,忘记验证真数为正,致使答案出错,做题时要注意转化等价.
分析:设a>1,可得外层函数是增函数,由此知内层函数在[
 ,4]也是增函数,由二次函数的性质可以得到关于参数的不等式,再由真数非负,即可求得参数的范围
,4]也是增函数,由二次函数的性质可以得到关于参数的不等式,再由真数非负,即可求得参数的范围解答:∵a>1
∴f(x)=logax是增函数
又函数f(x)=loga(ax2-x)在区间[
 ,4]上是增函数
,4]上是增函数∴ax2-x在区间[
 ,4]上是增函数,且当x=
,4]上是增函数,且当x= 时函数值为正
时函数值为正∴
 解得a>2
解得a>2故答案为(2,+∞)
点评:本题考查对数函数的单调性与特殊点,解本题的关键是根据复合函数的单调性判断出内层函数的单调性,由二次的性质得出参数的不等式,解出参数的范围,本题有一易错点,忘记验证真数为正,致使答案出错,做题时要注意转化等价.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
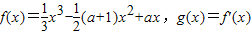 是函数f(x)的导函数,其中实数a是不等1的常数.
是函数f(x)的导函数,其中实数a是不等1的常数. ,4]上是增函数,则a的取值范围是 .
,4]上是增函数,则a的取值范围是 .