题目内容
19．
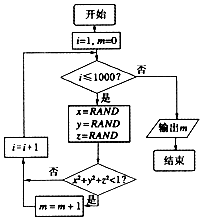我们可以用随机模拟的方法估计π的值，如图程序框图表示其基本步骤（函数RAND是产生随机数的函数，它能随机产生（0，1）内的任何一个实数）．若输出的结果为521，则由此可估计π的近似值为（ ）| A． | 3.119 | B． | 3.126 | C． | 3.132 | D． | 3.151 |
分析 我们可分析出程序的功能是利用随机模拟实验的方法求任取（0，1）上的x，y，z，求x2+y2+z2＜1的概率，计算x2+y2+z2＜1发生的概率为$\frac{4}{3}π•{1}^{3}•\frac{1}{8}$=$\frac{π}{6}$，代入几何概型公式，即可得到答案．
解答 解：x2+y2+z2＜1发生的概率为$\frac{4}{3}π•{1}^{3}•\frac{1}{8}$=$\frac{π}{6}$，当输出结果为521时，i=1001，m=521，x2+y2+z2＜1发生的概率为P=$\frac{521}{1000}$，∴$\frac{521}{1000}$=$\frac{π}{6}$，即π=3.126，
故选B．
点评 本题考查的知识点是程序框图，其中根据已知中的程序流程图分析出程序的功能，并将问题转化为几何概型问题是解答本题的关键，本题属于基本知识的考查．
练习册系列答案
相关题目
9．已知函数f（x）=$\left\{\begin{array}{l}{sin（\frac{π}{2}x）-1，x＜0}\\{lo{g}_{a}x（a＞0，且a≠1），x＞0}\end{array}\right.$的图象上关于y轴对称的点至少有3对，则实数a的取值范围是（ ）
| A． | $（0\;，\;\;\frac{{\sqrt{3}}}{3}）$ | B． | $（\frac{{\sqrt{5}}}{5}\;，\;\;1）$ | C． | $（\frac{{\sqrt{3}}}{3}\;，\;\;1）$ | D． | $（0\;，\;\;\frac{{\sqrt{5}}}{5}）$ |
10．函数 f （ x）=sin x+ex，则 f'（0）的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 0 |
7．计算$\underset{lim}{△x→0}$$\frac{sin（\frac{π}{6}+△x）-sin\frac{π}{6}}{△x}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
14．下列结构图中要素之间表示从属关系的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
11．已知a，b，c分别为△ABC三个内角A，B，C的对边，（a+b）（sinA-sinB）=（c-b）sinC，∠A=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
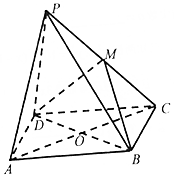如图，点P是菱形ABCD所在平面外一点，∠BAD=60°，△PCD是等边三角形，AB=2，PA=2$\sqrt{2}$，M是PC的中点．