题目内容
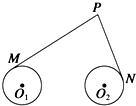 如图所示,圆O1和圆O2的半径都等于1,|O1O2|=6,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得|PM|=
如图所示,圆O1和圆O2的半径都等于1,|O1O2|=6,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得|PM|=| 3 |
考点:轨迹方程
专题:计算题,直线与圆
分析:建立直角坐标系,设P点坐标,列方程,化简,即可得到结果.
解答:
 解:以O1O2的中点O为原点,O1O2所在的直线为x轴,建立平面直角坐标系,则O1(-3,0),O2(3,0),
解:以O1O2的中点O为原点,O1O2所在的直线为x轴,建立平面直角坐标系,则O1(-3,0),O2(3,0),
由已知PM=
PN,得PM2=3PN2.
因为两圆的半径均为1,所以PO12-1=3(PO22-1).
设P(x,y),则(x+3)2+y2-1=3[(x-3)2+y2-1],
即(x-6)2+y2=28,
所以所求轨迹方程为(x-6)2+y2=28.
 解:以O1O2的中点O为原点,O1O2所在的直线为x轴,建立平面直角坐标系,则O1(-3,0),O2(3,0),
解:以O1O2的中点O为原点,O1O2所在的直线为x轴,建立平面直角坐标系,则O1(-3,0),O2(3,0),由已知PM=
| 3 |
因为两圆的半径均为1,所以PO12-1=3(PO22-1).
设P(x,y),则(x+3)2+y2-1=3[(x-3)2+y2-1],
即(x-6)2+y2=28,
所以所求轨迹方程为(x-6)2+y2=28.
点评:本题是典型的求轨迹方程的方法.是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若双曲线
-
=1的一条渐近线与直线3x-y+1=0平行,则此双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、2
| ||
| C、3 | ||
D、
|
确定结论“X与Y有关系”的可信度为99.5%时,则随机变量的观测值K必须( )
| A、小于10.828 |
| B、大于7.879 |
| C、小于6.635 |
| D、大于3.841 |
 已知函数f(x)=Asin2x(A>0)的部分图象,如图所示,
已知函数f(x)=Asin2x(A>0)的部分图象,如图所示,