题目内容
定义在R上的函数f(x)满足对任意x,y∈R恒有f(xy)=f(x)+f(y),且f(x)不恒为0.若x大于等于0时,f(x)为增函数,求满足不等式f(x+1)-f(2-x)≤0的x的取值集合.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:令x=y=1可得f(1)=0;再令x=y=-1,可得f(-1)=0;再令x=-1代入得f(-y)=f(y),所以函数f(x)是偶函数;再将f(x+1)-f(2-x)≤0变形为f(x+1)≤f(2-x),结合偶函数的性质可得到不含“f”符号的关于x的不等式,解之即可.
解答:
解:令x=y=1代入f(xy)=f(x)+f(y),可得f(1)=0,
同理令x=y=-1,可得f(-1)=0,
再令x=-1代入f(xy)=f(x)+f(y),得f(-y)=f(y),所以函数f(x)是偶函数;
f(x+1)-f(2-x)≤0可化为f(x+1)≤f(2-x),
又∵x≥0时,f(x)为增函数,
结合偶函数的图象性质可知,当自变量取值的绝对值越小时,函数值越小,
∴|x+1|≤|2-x|,
∴(x+1)2≤(2-x)2,解得x≤
,
∴所求集合为{x|x≤
}.
同理令x=y=-1,可得f(-1)=0,
再令x=-1代入f(xy)=f(x)+f(y),得f(-y)=f(y),所以函数f(x)是偶函数;
f(x+1)-f(2-x)≤0可化为f(x+1)≤f(2-x),
又∵x≥0时,f(x)为增函数,
结合偶函数的图象性质可知,当自变量取值的绝对值越小时,函数值越小,
∴|x+1|≤|2-x|,
∴(x+1)2≤(2-x)2,解得x≤
| 1 |
| 2 |
∴所求集合为{x|x≤
| 1 |
| 2 |
点评:此类问题一般先利用赋值法求出特殊点的函数值,判断函数的奇偶性等性质,再借助于图象得直观性的得到我们需要的隐含条件,最终得到关于x的具体的不等式,解之即可;这个题利用了偶函数与单调性之间的关系构造了关于x的不等式,最后不要忽视结果要写成集合形式.

练习册系列答案
相关题目
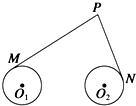 如图所示,圆O1和圆O2的半径都等于1,|O1O2|=6,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得|PM|=
如图所示,圆O1和圆O2的半径都等于1,|O1O2|=6,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得|PM|=