题目内容
已知函数 的图象如图,直线
的图象如图,直线 在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为
在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为 .
.
(1)求 的解析式;
的解析式;
(2)若常数 ,求函数
,求函数 在区间
在区间 上的最大值.
上的最大值.
(1) ;
;
(2)当 时,
时, ;当
;当 时,
时, .
.
解析试题分析:(1)由条件知, ,
, ,代入可得
,代入可得 、
、 .再用定积分表示出所围成的区域(阴影)面积,由面积为
.再用定积分表示出所围成的区域(阴影)面积,由面积为 解得
解得 ,从而得到
,从而得到 的解析式;(2)由(1)知
的解析式;(2)由(1)知 ,再列出
,再列出 ,的取值变化情况,又
,的取值变化情况,又 ,结合图像即可得当
,结合图像即可得当 时,
时, ;当
;当 时,
时, .
.
试题解析:(1)由 得
得 , 2分
, 2分 .由
.由 得
得 , 4分
, 4分
∴ ,则易知图中所围成的区域(阴影)面积为
,则易知图中所围成的区域(阴影)面积为
从而得 ,∴
,∴ . 8分
. 8分
(2)由(1)知 .
. 的取值变化情况如下:
的取值变化情况如下: 



2 







单调
递增极大值 
 练习册系列答案
练习册系列答案
智慧测评高中新课标同步导学系列答案
新梦想导学练系列答案
中考零距离系列答案
中华活页文选初中文言文精讲精练系列答案
自能导学系列答案
中考制高点系列答案
英语指导系列答案
龙江中考系列答案
状元陪练系列答案
2016中考168系列答案
相关题目
 ,其中
,其中 .
. ,求
,求 在
在 的最小值;
的最小值; 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围; ,使得当
,使得当 时,不等式
时,不等式 恒成立.
恒成立. ,其中
,其中 .
. 时判断
时判断 的单调性;
的单调性; 在其定义域为增函数,求正实数
在其定义域为增函数,求正实数 的取值范围;
的取值范围; ,当
,当 时,若
时,若 ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围. .
.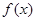 的单调区间和极值;
的单调区间和极值;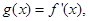 直线
直线 与曲线
与曲线 相交于
相交于 不同两点,若
不同两点,若 试证明
试证明 .
. ,数列
,数列 ,满足0<
,满足0< <1,
<1, ,数列
,数列 满足
满足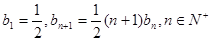 ,
, 的单调区间;
的单调区间; <
< <1;
<1; 且
且 ,则当n≥2时,求证:
,则当n≥2时,求证: >
>
 ,
, .
. 的单调递增区间;
的单调递增区间; 为函数
为函数 处的切线的斜率恒大于
处的切线的斜率恒大于 ,
, 的取值范围.
的取值范围.
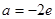 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值; 在[1,4]上是减函数,求实数
在[1,4]上是减函数,求实数 的取值范围.
的取值范围. ,曲线
,曲线 过点
过点 ,且在
,且在 点处的切线斜率为2.
点处的切线斜率为2. .
. (其中
(其中 ),且方程
),且方程 的两个根分别为
的两个根分别为 、
、 .
. 且曲线
且曲线 过原点时,求
过原点时,求 的解析式;
的解析式; 无极值点,求
无极值点,求 的取值范围.
的取值范围.