题目内容
在直角坐标系xOy中,已知定点A(-1,0),动点C在射线y=-x(x≤0)上运动,动点D在射线y=x(x≥0)上运动,且满足
•
=0.
(1)是否存在点C,使|
|=
,若存在,求出C点坐标;若不存在,请说明理由;
(2)求证∠ACD是为定值,且求出∠ACD的大小.
| AC |
| AD |
(1)是否存在点C,使|
| CD |
| 10 |
(2)求证∠ACD是为定值,且求出∠ACD的大小.
考点:平面向量数量积的运算
专题:计算题,解三角形,平面向量及应用
分析:(1)假设存在点C,使|
|=
.可设C(m,-m),D(n,n),(m≤0,n≥0),由向量的数量积的坐标运算和向量模的公式,可得m,n方程,解出即可;
(2)运用向量垂直的条件:数量积为0,求出AC,AD的长,判断三角形ACD的形状,进而得到∠ACD为定值,求出即可.
| CD |
| 10 |
(2)运用向量垂直的条件:数量积为0,求出AC,AD的长,判断三角形ACD的形状,进而得到∠ACD为定值,求出即可.
解答:
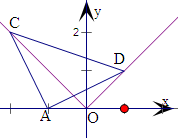 解:(1)假设存在点C,使|
解:(1)假设存在点C,使|
|=
.
可设C(m,-m),D(n,n),(m≤0,n≥0),
=(m+1,-m),
=(n+1,n),
由于
•
=0,则(m+1)(n+1)-mn=0,
即m+n=-1①
又|
|=
,即
=
,
化简得m2+n2=5,②
由①②可得,m=-2,n=1.
则存在点C(-2,2),使|
|=
.
(2)证明:由
•
=0,则AC⊥AD,
可设C(m,-m),D(n,n),(m≤0,n≥0),
=(m+1,-m),
=(n+1,n),
由于
•
=0,则(m+1)(n+1)-mn=0,
即m+n=-1,
则|
|=
=
,
|
|=
=
=
,
即有|
|=|
|,
则△ACD为等腰直角三角形,
则有∠ACD是为定值,且为45°.
 解:(1)假设存在点C,使|
解:(1)假设存在点C,使|| CD |
| 10 |
可设C(m,-m),D(n,n),(m≤0,n≥0),
| AC |
| AD |
由于
| AC |
| AD |
即m+n=-1①
又|
| CD |
| 10 |
| (n-m)2+(n+m)2 |
| 10 |
化简得m2+n2=5,②
由①②可得,m=-2,n=1.
则存在点C(-2,2),使|
| CD |
| 10 |
(2)证明:由
| AC |
| AD |
可设C(m,-m),D(n,n),(m≤0,n≥0),
| AC |
| AD |
由于
| AC |
| AD |
即m+n=-1,
则|
| AC |
| (m+1)2+m2 |
| 2m2+2m+1 |
|
| AD |
| (n+1)2+n2 |
| (-1-m+1)2+(-1-m)2 |
| 2m2+2m+1 |
即有|
| AC |
| AD |
则△ACD为等腰直角三角形,
则有∠ACD是为定值,且为45°.
点评:本题考查向量的数量积的坐标表示,主要考查向量垂直的条件和向量模的公式,考查三角形的形状的判断进而求内角,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲、乙、丙、丁、戊五名应届师范毕业生分配到A,B,C三所学校任教,其中A学校和B学校要2人,C学校要1人,且甲、乙两人不能到同一所学校任教,则不同的分配方案的种数为( )
| A、30 | B、48 | C、24 | D、36 |
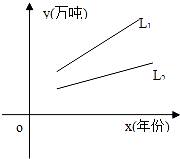 对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述:
对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述: