题目内容
已知函数f(x)=x2-4x+a+3,a∈R.
(1)若函数f(x)在(-∞,+∞)上至少有一个零点,求a的取值范围;
(2)若函数f(x)在[a+1,a+2]上的最大值为3,求a的值.
(1)若函数f(x)在(-∞,+∞)上至少有一个零点,求a的取值范围;
(2)若函数f(x)在[a+1,a+2]上的最大值为3,求a的值.
考点:二次函数在闭区间上的最值,函数的零点
专题:函数的性质及应用
分析:(1)由判别式大于或等于零,求得a的范围.
(2)函数f(x)的图象对称轴方程为x=2,再分对称轴在区间中间值的左侧、右侧两种情况,分别求得函数的最大值,再根据函数的最大值为3,求得a的值.
(2)函数f(x)的图象对称轴方程为x=2,再分对称轴在区间中间值的左侧、右侧两种情况,分别求得函数的最大值,再根据函数的最大值为3,求得a的值.
解答:
解:(1)由函数f(x)=x2-4x+a+3,a∈R在(-∞,+∞)上至少有一个零点,可得△=16-4(a+3)≥0,
求得a≤1.
(2)由于函数f(x)的图象对称轴方程为x=2,当2≤
,
即a≥
时,f(x)在[a+1,a+2]上的最大值为f(a+2)=a2+a-1=3,求得a=
.
当2>
,即 a<
时,f(x)在[a+1,a+2]上的最大值为f(a)=a2-3a+3=3,求得a=0.
综上,a=
,或a=0.
求得a≤1.
(2)由于函数f(x)的图象对称轴方程为x=2,当2≤
| a+1+a+2 |
| 2 |
即a≥
| 1 |
| 2 |
-1+
| ||
| 2 |
当2>
| a+1+a+2 |
| 2 |
| 1 |
| 2 |
综上,a=
-1+
| ||
| 2 |
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属基础题.

练习册系列答案
相关题目
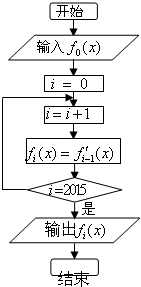
在如图所示的程序框图中,若f0(x)=xex,则输出的结果是( )

| A、2016ex+xex |
| B、2015ex+xex |
| C、2014ex+xex |
| D、2013ex+x |
在△ABC中,角A、B、C所对的边分别为a,b,c,且
=
,则角C是( )
| sinA |
| a |
| ||
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
若α是第一象限的角,则
所在的象限是( )
| α |
| 2 |
| A、第一象限 |
| B、第一、二象限 |
| C、第一、三象限 |
| D、第一、四象限 |