题目内容
若集合A={x||x|≤1}，B={x|
≤0}，则A∩B为（ ）
| x-2 |
| x |
| A、[-1，0） |
| B、（0，1] |
| C、[0，2] |
| D、[0，1] |
考点：交集及其运算
专题：集合
分析：利用交集的定义和不等式的性质求解．
解答：
解：∵集合A={x||x|≤1}={x|-1≤x≤1}，
B={x|
≤0}={x|0＜x≤2}，
∴A∩B={x|0＜x≤1}=（0，1]．
故选：B．
B={x|
| x-2 |
| x |
∴A∩B={x|0＜x≤1}=（0，1]．
故选：B．
点评：本题考查交集的求法，是基础题，解题时要认真审题，注意不等式性质的合理运用．
练习册系列答案
相关题目
已知a=log23.6，b=log33.6，c=log23.9，则正确的是（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞b＞a |
| D、c＞a＞b |
已知函数f（x）=
，那么f[f（-2）]=（ ）
|
| A、-16 | B、16 | C、2 | D、-2 |
如图，在三棱锥A-BCD中，AB=CD=6，AC=BD=8，BC=10，且A在平面BCD上的投影O恰好在BD上．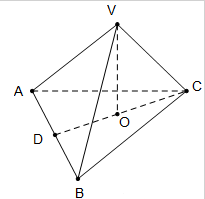
如图，三棱锥V-ABC中，VO⊥平面ABC，O∈CD，AB=4，AD=BD，VA=VB=