题目内容
如图所示,边长为(1)求cos〈![]() 〉;
〉;
(2)若BE⊥VC,求cos〈![]() 〉.
〉.
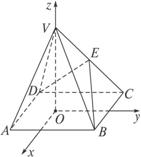
解析:(1)建立如图所示坐标系,过O作Oy∥DC,Ox∥AD,分别以Ox、Oy、OV为x轴、y轴、z轴,则B(a,a,0), ![]() =
=![]() (
(![]() +
+![]() ),即E(-
),即E(-![]() ,
,![]() ,
,![]() ),D(-a,-a,0).
),D(-a,-a,0).

由此得![]() =(-
=(-![]() a,-
a,-![]() ,
,![]() ),
), ![]() =(
=(![]() ,
,![]() ,
,![]() ).
).
∴![]() ·
·![]() =(-
=(-![]() a)(
a)(![]() )+(-
)+(-![]() )(
)(![]() a)+(
a)+( ![]() )(
)(![]() )=
)=![]() .
.
|![]() |=|
|=|![]() |=
|=![]() ,
,
∴cos〈![]() ,
,![]() 〉=
〉=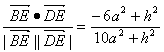 .
.
(2)由E是VC的中点,又BE⊥VC有![]() ·
·![]() =0,
=0,
∵V(0,0,h),C(-a,a,0),∴![]() =(-a,a,-h).
=(-a,a,-h).
∴(-![]() a,
a,![]() ,
,![]() )(-a,a,-h)=0,即
)(-a,a,-h)=0,即![]() a2-
a2-![]() =0.∴h=
=0.∴h=![]() .
.
这时cos〈![]() ,
,![]() 〉=
〉=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 某三棱柱侧棱和底面垂直,底面边长均为a,侧棱长为2a,其体积为
某三棱柱侧棱和底面垂直,底面边长均为a,侧棱长为2a,其体积为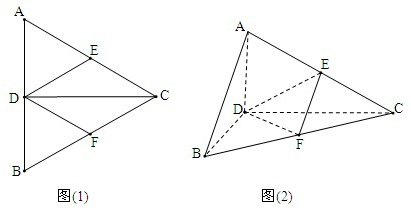 如图(1)所示,正△ABC的边长为2a,CD是AB边上的高,E,F分别是AC,BC的中点.现将△ABC沿CD翻折,使翻折后平面ACD⊥平面BCD(如图(2)),
如图(1)所示,正△ABC的边长为2a,CD是AB边上的高,E,F分别是AC,BC的中点.现将△ABC沿CD翻折,使翻折后平面ACD⊥平面BCD(如图(2)), (2012•杨浦区二模)如图所示,直四棱柱ABCD-A1B1C1D1的侧棱AA1长为a,底面ABCD是边长AB=2a,BC=a的矩形,E为C1D1的中点.
(2012•杨浦区二模)如图所示,直四棱柱ABCD-A1B1C1D1的侧棱AA1长为a,底面ABCD是边长AB=2a,BC=a的矩形,E为C1D1的中点.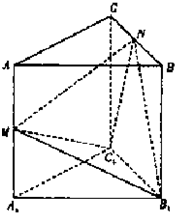 (2010•武汉模拟)如图所示,在正三棱柱ABC-A1B1C1中,底面ABC的边长为2a,侧棱AA1=2a,M、N分别为AA1、BC中点
(2010•武汉模拟)如图所示,在正三棱柱ABC-A1B1C1中,底面ABC的边长为2a,侧棱AA1=2a,M、N分别为AA1、BC中点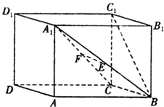 如图所示,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长为a,∠ABC=60°,E、F分别是A1B、A1C的中点.
如图所示,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长为a,∠ABC=60°,E、F分别是A1B、A1C的中点.