题目内容
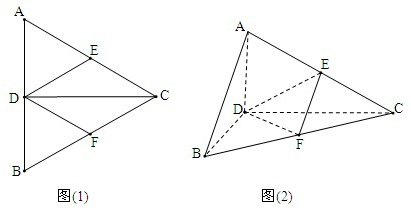 如图(1)所示,正△ABC的边长为2a,CD是AB边上的高,E,F分别是AC,BC的中点.现将△ABC沿CD翻折,使翻折后平面ACD⊥平面BCD(如图(2)),
如图(1)所示,正△ABC的边长为2a,CD是AB边上的高,E,F分别是AC,BC的中点.现将△ABC沿CD翻折,使翻折后平面ACD⊥平面BCD(如图(2)),(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求三棱锥C-DEF的体积.
分析:(1)判断:AB∥平面DEF,再由直线与平面平行的判定定理进行证明.
(2)过点E作EM⊥DC于点M,由面ACD⊥面BCD,面ACD∩面BCD=CD,而EM?面ACD,知EM是三棱锥E-CDF的高,由此能求出三棱锥C-DEF的体积.
(2)过点E作EM⊥DC于点M,由面ACD⊥面BCD,面ACD∩面BCD=CD,而EM?面ACD,知EM是三棱锥E-CDF的高,由此能求出三棱锥C-DEF的体积.
解答:解:(1)判断:AB∥平面DEF,(2分)
证明:因在△ABC中,E,F分别是AC,BC的中点,
∴EF∥AB,(5分)
又因AB?平面DEF,
∴EF?平面DEF,(6分)
所以AB∥平面DEF,(7分)
(2)过点E作EM⊥DC于点M,
∵面ACD⊥面BCD,面ACD∩面BCD=CD,而EM?面ACD
故EM⊥平面BCD 于是EM是三棱锥E-CDF的高,(9分)
又△CDF的面积为S△CDF=
S△BCD=
•
•CD•BD=
•a=
a2,
EM=
AD=
a,(11分)
故三棱锥C-DEF的体积VC-DEF=VE-CDF=
S△CDF•EM=
•
•
a=
.(14分)
证明:因在△ABC中,E,F分别是AC,BC的中点,
∴EF∥AB,(5分)
又因AB?平面DEF,
∴EF?平面DEF,(6分)
所以AB∥平面DEF,(7分)
(2)过点E作EM⊥DC于点M,
∵面ACD⊥面BCD,面ACD∩面BCD=CD,而EM?面ACD
故EM⊥平面BCD 于是EM是三棱锥E-CDF的高,(9分)
又△CDF的面积为S△CDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| (2a)2-a2 |
| ||
| 4 |
EM=
| 1 |
| 2 |
| 1 |
| 2 |
故三棱锥C-DEF的体积VC-DEF=VE-CDF=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 24 |
点评:本题考查直线与平面的位置关系的判断,考查三棱锥的体积的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 如图(1)所示,正△ABC的边长为2a,CD是AB边上的高,E,F分别是AC,BC的中点.现将△ABC沿CD翻折,使翻折后平面ACD⊥平面BCD(如图(2)),
如图(1)所示,正△ABC的边长为2a,CD是AB边上的高,E,F分别是AC,BC的中点.现将△ABC沿CD翻折,使翻折后平面ACD⊥平面BCD(如图(2)),

