Question

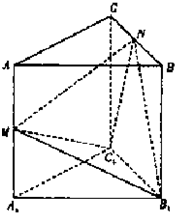（2010•武汉模拟）如图所示，在正三棱柱ABC-A₁B₁C₁中，底面ABC的边长为2a，侧棱AA₁=2a，M、N分别为AA₁、BC中点
（1）求四面体C₁-MNB₁体积；
（2）求直线MC₁与平面MNB₁所成角正弦值．

Answer 1

分析：（1）对于四面体求体积，可以也即三棱锥求体积，可把其中一个面作为底面，与底面相对的顶点作为三棱锥的顶点，用

1

3

的底面积乘高即可．在本题中，因为三角形B₁C₁N的面积比较好求，且M点到平面B₁C₁N的距离为2a，所以把M点作为三棱锥的顶点来求体积．
（2）欲求直线MC₁与平面MNB₁所成角正弦值，先找到该角，直线与平面所成角，即直线与它在平面上的射影所成角，过直线MC₁上点M作平面MNB₁的垂线，则垂线段即为M到平面的距离，直线MC₁与平面MNB₁所成角正弦值为垂线段与线段MC₁的比．

解答：解：（1）在正三棱柱ABC-A₁B₁C₁中，AA₁∥BC₁
从而可得VN-A1B1C1=

1

3

(

1

2

•2a•2a•sin60°)•2a=

2 3

3

a3．
（2）对于△MNB₁，B₁N=B₁M=

5

a，MN=2a
则△MNB₁面积S=

1

2

•2a•2a=2a²
 设C₁到平面MNB₁之距为d，则由VC1-MNB1=VN-B1C1N知：

1

3

(S△MNB1)•d=

2 3

3

a，∴

1

3

•2a2•d=

2 3

3

a2得到d=

3

a，
设MC₁与平面MNB₁所成角为θ，
则sinθ=

d

MC1

=

3 a

5 a

=

15

5

．

点评：本题主要考查了三棱锥体积的求法，以及直线与平面所成角的求法，求体积时注意等体积法的应用，求线面角的关键在与找到线面角的平面角．