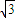题目内容
设双曲线 -
- =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,且它的一条准线与抛物线y2=4x的准线重合,则此双曲线的方程为
,且它的一条准线与抛物线y2=4x的准线重合,则此双曲线的方程为
- A.
 -
-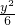 =1
=1 - B.
 -
- =1
=1 - C.
 -
- =1
=1 - D.
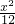 -
- =1
=1
A
分析:利用抛物线的准线方程求出其准线;据双曲线的离心率及准线方程公式列出方程,求出a,c的值;利用双曲线中的三参数的故选求出b的值;利用双曲线的渐近线方程公式求出双曲线的渐近线方程.
解答:抛物线y2=4x的准线为x=-1,
所以对双曲线
有 ,
,
 ,
,
解得
∴b2=c2-a2=6
则此双曲线的方程为 -
-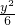 =1
=1
故选A.
点评:本题考查双曲线的离心率公式为: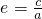 ;准线方程为
;准线方程为  ;渐近线方程与焦点的位置有关.
;渐近线方程与焦点的位置有关.
分析:利用抛物线的准线方程求出其准线;据双曲线的离心率及准线方程公式列出方程,求出a,c的值;利用双曲线中的三参数的故选求出b的值;利用双曲线的渐近线方程公式求出双曲线的渐近线方程.
解答:抛物线y2=4x的准线为x=-1,
所以对双曲线

有
 ,
, ,
,解得

∴b2=c2-a2=6
则此双曲线的方程为
 -
-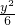 =1
=1故选A.
点评:本题考查双曲线的离心率公式为:
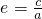 ;准线方程为
;准线方程为  ;渐近线方程与焦点的位置有关.
;渐近线方程与焦点的位置有关. 
练习册系列答案
相关题目
 -
- =1(a>0,b>0)的虚轴长为2,焦距为2
=1(a>0,b>0)的虚轴长为2,焦距为2 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )


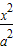 -
-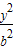 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为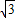 ,且它的一条准线与抛物线y2=4x的准线重合,则此双曲线的方程为( )
,且它的一条准线与抛物线y2=4x的准线重合,则此双曲线的方程为( )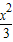 -
- =1
=1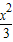 -
- =1
=1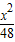 -
- =1
=1 -
-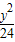 =1
=1 =1(a>0,b>0)的右顶点为A,P为双曲线上的一个动点(不是顶点),从点A引双曲线的两条渐近线的平行线,与直线OP分别交于Q,R两点,其中O为坐标原点,则|OP|2与|OQ|•|OR|的大小关系为( )
=1(a>0,b>0)的右顶点为A,P为双曲线上的一个动点(不是顶点),从点A引双曲线的两条渐近线的平行线,与直线OP分别交于Q,R两点,其中O为坐标原点,则|OP|2与|OQ|•|OR|的大小关系为( )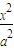 -
-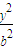 =1(a>0,b>0)的右焦点为F,右准线l与两条渐近线交于P、Q两点,如果△PQF是直角三角形,则双曲线的离心率e= .
=1(a>0,b>0)的右焦点为F,右准线l与两条渐近线交于P、Q两点,如果△PQF是直角三角形,则双曲线的离心率e= .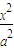 -
-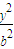 =1(a>0,b>0)的渐近线与曲线y=x2+
=1(a>0,b>0)的渐近线与曲线y=x2+ 相切,则该双曲线的离心率等于( )
相切,则该双曲线的离心率等于( )