题目内容
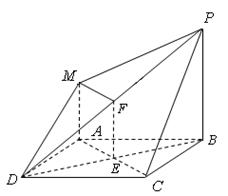 如图,四边形
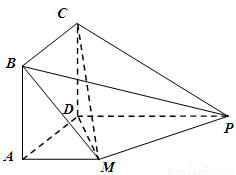
如图,四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,
,![]() 求证:(1)平面
求证:(1)平面![]() ∥平面
∥平面![]() ;(2)平面
;(2)平面![]() ^平面
^平面![]()
(Ⅰ) 略 (Ⅱ) 略
解析:
(1)证明:因为PB^平面ABCD,MA^平面ABCD,所以PB∥MA.因PB??平面BPC,MA (/平面BPC,所以MA∥平面BPC.同理DA∥平面BPC,因为MA??平面AMD,AD??平面AMD,MA∩AD=A,所以平面AMD∥平面BPC.(6分)
(2)连接AC,设AC∩BD=E,取PD中点F,连接EF,MF.因ABCD为正方形,所以E为BD中点.因为F为PD中点,所以EF∥=PB.因为AM∥=PB,所以AM∥=EF.所以AEFM为平行四边形.所以MF∥AE.因为PB^平面ABCD,AE??平面ABCD,所以PB^AE.所以MF^PB.因为ABCD为正方形,所以AC^BD.所以MF^BD.所以MF^平面PBD.又MF??平面PMD.所以平面PMD^平面PBD.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目

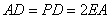





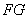
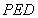
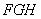
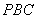
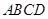 是正方形,
是正方形,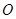 为对角线
为对角线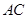 和
和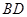 的交点,
的交点,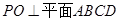 ,
, 为
为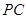 的中点;
的中点;
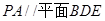 ;
;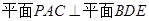 .
.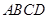 是正方形,
是正方形,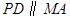 ,
,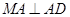 ,
, ,
,
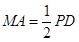 .
.
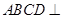 平面
平面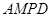 ;
;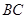 与
与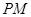 所成的角为
所成的角为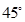 ,求二面角
,求二面角 的余弦值.
的余弦值.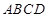 是正方形,
是正方形,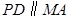 ,
,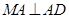 ,
,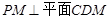 ,
,
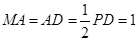
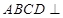 平面
平面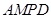 ;
;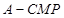 的高
的高
