题目内容
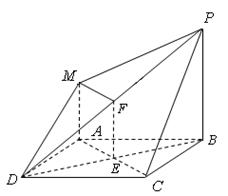
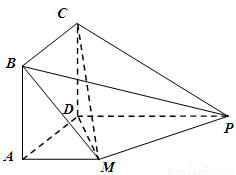
如图,四边形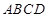 是正方形,
是正方形,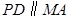 ,
,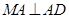 ,
,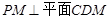 ,
,
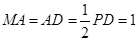
(Ⅰ)求证:平面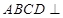 平面
平面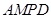 ;
;
(Ⅱ)求三棱锥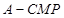 的高
的高

【答案】
①见解析 ②
【解析】
试题分析:(I)要证面面垂直,只要证明线面垂直,只要证明线线垂直:即找到直线 (Ⅱ)因为
(Ⅱ)因为 ,所以求点面距离转化为等体积方法计算,容易求出三角形
,所以求点面距离转化为等体积方法计算,容易求出三角形 的面积与高
的面积与高 的值, 再计算出三角形
的值, 再计算出三角形 的面积即可
的面积即可
试题解析:(Ⅰ)
 平面
平面 ,且
,且 平面
平面 ,
,

 ,
,
又 是正方形,
是正方形,
 ,而梯形
,而梯形 中
中 与
与 相交,
相交,
 平面
平面 ,
,
又 平面
平面 ,
,
 平面
平面 平面
平面 4分
4分
(Ⅱ)设三棱锥 的高为
的高为 ,
,
已证 平面
平面 ,又
,又 ,则
,则 ,
, ,
,
由已知 ,得
,得 ,
, ,
, , 6分
, 6分
故 ,
,
 8分
8分


则 10分
10分

 12分
12分
故三棱锥 的高为
的高为
(其他做法参照给分)
考点:1 线面位置关系;2 垂直的判定与性质;3 等体积法求椎体的高

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 如图,四边形
如图,四边形
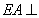

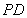
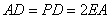

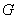
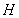




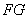
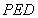
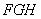
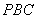
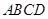 是正方形,
是正方形,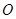 为对角线
为对角线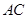 和
和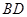 的交点,
的交点,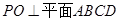 ,
, 为
为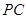 的中点;
的中点;
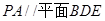 ;
;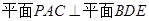 .
.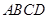 是正方形,
是正方形,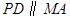 ,
,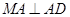 ,
, ,
,
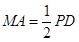 .
.
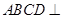 平面
平面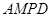 ;
;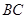 与
与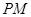 所成的角为
所成的角为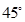 ,求二面角
,求二面角 的余弦值.
的余弦值.