题目内容
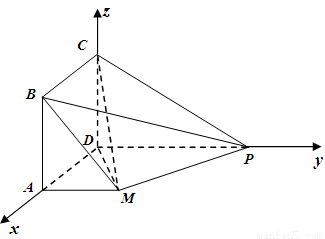
如图,四边形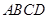 是正方形,
是正方形,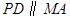 ,
,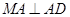 ,
, ,
,
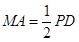 .
.
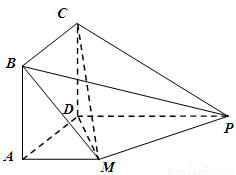
(Ⅰ)求证:平面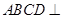 平面
平面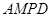 ;
;
(Ⅱ)若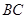 与
与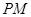 所成的角为
所成的角为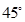 ,求二面角
,求二面角 的余弦值.
的余弦值.
【答案】
①见解析②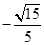
【解析】
试题分析:(I)要证面面垂直,只要证明线面垂直,只要证明线线垂直:即找到直线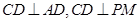 (II)由于
(II)由于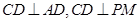 选取
选取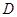 为坐标原点建立空间直角坐标系,由于底面直角梯形只有上下底边的关系,直角腰边长
为坐标原点建立空间直角坐标系,由于底面直角梯形只有上下底边的关系,直角腰边长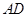 需要用
需要用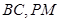 成
成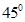 角这个等式确定的,进一步计算出多面体顶点坐标,利用空间向量计算出两个平面的法向量,再求二面角的余弦值.
角这个等式确定的,进一步计算出多面体顶点坐标,利用空间向量计算出两个平面的法向量,再求二面角的余弦值.
试题解析:(I)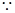
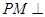 平面
平面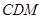 ,且
,且 平面
平面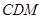 ,
,
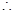
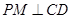 ,
,
又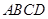 是正方形,
是正方形,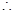
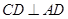 ,而梯形
,而梯形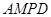 中
中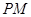 与
与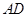 相交,
相交,
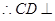 平面
平面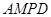 ,
,
又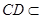 平面
平面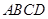 ,
,
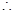 平面
平面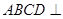 平面
平面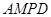 4分
4分
(II)
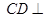 平面
平面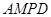 ,则
,则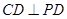 ,
,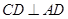 ,
,
又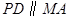 ,
,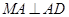 ,
,
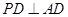 ,
,
以点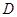 为原点,
为原点,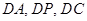 依次为
依次为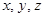 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
不妨设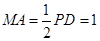 ,
,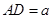 .
.
则 ,
,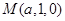 ,
,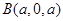 ,
,
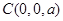 ,
,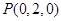 .6分
.6分
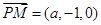 ,
,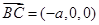 ,
,
由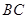 与
与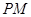 所成的角为
所成的角为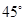 ,
,
得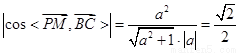
解得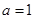 . .8分
. .8分
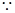
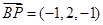 ,
,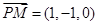 ,
,
求得平面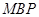 的一个法向量是
的一个法向量是
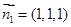 ; ..9分
; ..9分
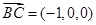 ,
,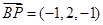 ,
,
求得平面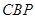 的一个法向量是
的一个法向量是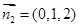 ; ..10分
; ..10分
则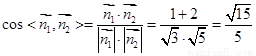 , ..11分
, ..11分
故二面角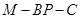 的余弦值为
的余弦值为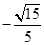 .12分
.12分
(其他做法参照给分)
考点:1.线面位置关系垂直的判定与性质;2.空间向量;3.异面直线成角;4二面角.

练习册系列答案
相关题目
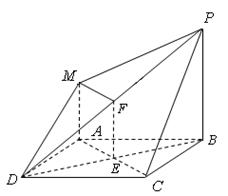 如图,四边形
如图,四边形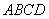
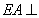

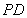
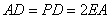

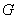
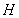




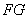
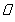
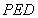
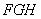
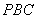
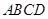 是正方形,
是正方形,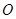 为对角线
为对角线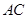 和
和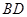 的交点,
的交点,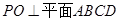 ,
, 为
为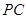 的中点;
的中点;
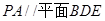 ;
;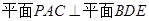 .
.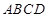 是正方形,
是正方形,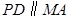 ,
,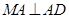 ,
,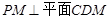 ,
,
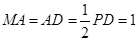
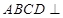 平面
平面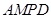 ;
;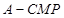 的高
的高
