题目内容

【题目】给出下列说法：

①集合与集合是相等集合；

②若函数的定义域为，则函数的定义域为；

③函数的单调减区间是；

④不存在实数m，使为奇函数；

⑤若，且，则.

其中正确说法的序号是（ ）

A.①③④B.②④⑤C.②③⑤D.①④⑤

【答案】D

【解析】

对①,分析集合表示的范围即可.

对②,根据定义域的定义求解判断即可.

对③,根据反比例函数的单调区间判定即可.

对④,根据奇函数的性质判定即可.

对⑤,根据递推公式求解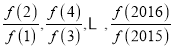的值再求和即可.

对①, 表示奇数的集合, 也表示奇数的集合,故成立.故①正确.

对②, 若函数的定义域为，则函数的定义域为解得定义域为,故②错误.

对③, 函数的单调减区间是和,不能写成.故③错误.

对④,因为故不存在实数m，使为奇函数,故④正确.

对⑤,因为,且,故,

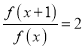即.故.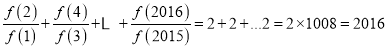

故⑤正确.

综上, ①④⑤正确.

故选：D

练习册系列答案
相关题目

【题目】设函数,

（1）若关于的不等式的解集为，求实数的值；

（2）求不等式的解集；

（3）若对于，恒成立，求实数的取值范围．

【题目】给出如下四个命题：①若“且”为假命题，则均为假命题；②命题“若，则”的否命题为“若，则”； ③“，则”的否定是“，则”；④在中，“”是“”的充要条件．其中正确的命题的个数是（ ）

A. 1B. 2C. 3D. 4

【题目】已知函数.

（1）若是函数的一个极值点，求实数的值；

（2）讨论函数的单调性.

（3）若对于任意的，当时，不等式恒成立，求实数的取值范围.

【题目】2019年，随着中国第一款5G手机投入市场，5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析，得到如下规律：每生产手机万台，其总成本为，其中固定成本为800万元，并且每生产1万台的生产成本为1000万元（总成本=固定成本+生产成本），销售收入万元满足

（1）将利润表示为产量万台的函数；

（2）当产量为何值时，公司所获利润最大？最大利润为多少万元？

【题目】已知函数．

（）若是函数的一个极值点，求实数的值．

（）设，当时，函数的图象恒不在直线的上方，求实数的取值范围．

【题目】已知数列｛an｝的前n项和Sn=2an-2(n∈Z+).

（1）求通项公式an；

（2）设，为数列｛bn｝的前n项和，求正整数k，使得对任意的n∈Z+，均有T4≥Tn；

（3）设，Rn为数列{cn}的前n项和，若对任意的n∈Z+，均有Rn<λ，求λ的最小值.

【题目】已知向量＝（2sin x，cos x），＝（－sin x,2sin x），函数f（x）＝·

（1）求f（x）的单调递增区间；

（2）在△ABC中，a，b，c分别是角A，B，C的对边，且f（C）＝1，c＝1，ab＝2，且a>b，求a，b的值．

【题目】某校举行汉字听写比赛，为了了解本次比赛成绩情况，从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数，满分100分)进行统计，请根据频率分布表中所提供的数据，解答下列问题：

（1）求的值；

（2）若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛，并从中选出2人做种子选手，求2人中至少有1人是第4组的概率.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网