题目内容
已知函数 .
.
(1)判断 奇偶性, 并求出函数
奇偶性, 并求出函数 的单调区间;
的单调区间;
(2)若函数 有零点,求实数
有零点,求实数 的取值范围.
的取值范围.
 .
.(1)判断
 奇偶性, 并求出函数
奇偶性, 并求出函数 的单调区间;
的单调区间; (2)若函数
 有零点,求实数
有零点,求实数 的取值范围.
的取值范围.(1) 是偶函数,
是偶函数, 的单调增区间是
的单调增区间是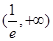 ,
,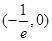 ;单调减区间是
;单调减区间是 ,
,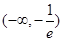 ,
,
(2)
 是偶函数,
是偶函数, 的单调增区间是
的单调增区间是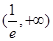 ,
,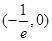 ;单调减区间是
;单调减区间是 ,
,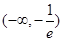 ,
,(2)

试题分析:解(1)
 定义域
定义域 在数轴上关于原点对称,
在数轴上关于原点对称, 且
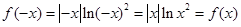 ,所以
,所以 是偶函数 2分
是偶函数 2分当
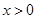 时,
时, 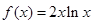 ,
, 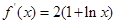
由
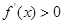 ,
, 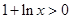 , 解得:
, 解得: 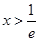 所以
所以 在
在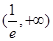 是增函数;
是增函数;由
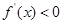 ,
, 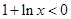 , 解得:
, 解得: 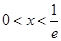 .所以
.所以 在
在 是减函数. 4分
是减函数. 4分因为
 是偶函数, 图象关于
是偶函数, 图象关于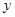 轴对称,所以, 当
轴对称,所以, 当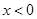 时,
时,  在
在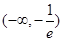 是减函数, 在
是减函数, 在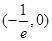 是增函数.
是增函数.所以,
 的单调增区间是
的单调增区间是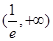 ,
,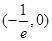 ;单调减区间是
;单调减区间是 ,
,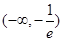 ,. 6分
,. 6分(2) 由
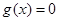 ,得
,得 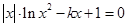 ,
, 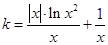
令
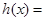
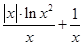 8分
8分当
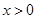 时,
时, 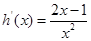 ,当
,当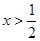 ,
, 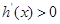 ,
, 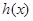 在
在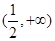 是增函数;
是增函数;当
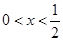 ,
, 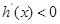 ,
, 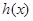 在
在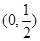 是减函数,
是减函数, 所以, 当
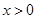 时,
时,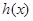 极小值是
极小值是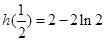 11分
11分因为
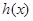 是奇函数,所以, 当
是奇函数,所以, 当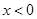 时,
时, 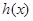 极大值是
极大值是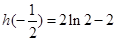
所以
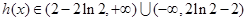 ,
, 即
 , 函数
, 函数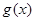 有零点. 14分
有零点. 14分点评:主要是考查了运用导数来判定函数单调性以及函数零点的综合运用,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
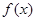
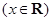 满足
满足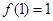 ,
,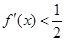 ,则不等式
,则不等式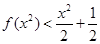 的解集为______.
的解集为______.
 ,且当
,且当
 满足
满足





 、
、 分别是定义在R上的奇函数和偶函数。当
分别是定义在R上的奇函数和偶函数。当 时,
时, 且
且 。则不等式
。则不等式 的解集是( )
的解集是( )




 及
及 ,
,
 两点连线的斜率为
两点连线的斜率为 ,问是否存在常数
,问是否存在常数 ,且
,且 ,当
,当 时有
时有 ,当
,当 时有
时有 ;若存在,求出
;若存在,求出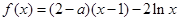 .
.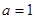 时,求
时,求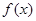 的单调区间;
的单调区间;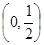 上无零点,求
上无零点,求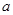 的最小值。
的最小值。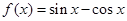 ,
, 为
为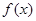 的导函数.
的导函数.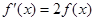 ,求
,求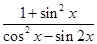 的值;
的值;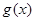 图象与
图象与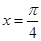 对称,△ABC的三个内角A、B、C所对的边长分别为
对称,△ABC的三个内角A、B、C所对的边长分别为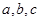 ,角A为
,角A为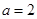 ,求△ABC面积的最大值.
,求△ABC面积的最大值. ,则
,则 =_______.
=_______. ,若
,若 ,则a的值等于 ( )
,则a的值等于 ( )


