题目内容
9.若cos($\frac{π}{8}$-α)=$\frac{1}{5}$,则cos($\frac{3π}{4}$+2α)的值为( )| A. | -$\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | -$\frac{23}{25}$ | D. | $\frac{23}{25}$ |
分析 利用诱导公式得出cos($\frac{π}{8}$-α)=sin($\frac{3π}{8}$+α),再利用二倍角公式求出cos($\frac{3π}{4}$+2α)的值.
解答 解:∵cos($\frac{π}{8}$-α)=sin[$\frac{π}{2}$-($\frac{π}{8}$-α)]
=sin($\frac{3π}{8}$+α)
=$\frac{1}{5}$,
∴cos($\frac{3π}{4}$+2α)=1-2sin2($\frac{3π}{8}$+α)
=1-2×${(\frac{1}{5})}^{2}$
=$\frac{23}{25}$.
故选:D.
点评 本题考查了三角恒等变换应用问题,是基础题目.

练习册系列答案
相关题目
20.若函数f(x)=sin(2x+$\frac{π}{6}$)+cos(2x-$\frac{π}{3}$),则f(x)的单调递增区间为( )
| A. | (kπ-$\frac{7π}{12}$,kπ-$\frac{π}{12}$),k∈Z | B. | (kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$),k∈Z | ||
| C. | (kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$),k∈Z | D. | (kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$),k∈Z |
17.已知集合A={x|x(x-2)=0},B={x∈Z|4x2-9≤0},则A∪B等于( )
| A. | {-2,-1,0,1} | B. | {-1,0,1,2} | C. | [-2,2] | D. | {0,2} |
7.设双曲线的实轴长为2a(a>0),一个焦点为F,虚轴的一个端点为B,如果原点到直线FB的距离恰好为实半轴长,那么双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
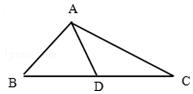 如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=$\frac{3\sqrt{6}}{8}$.
如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=$\frac{3\sqrt{6}}{8}$.