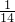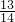题目内容
已知泊数f(x)=sinxcosx-
(I)求f(x)的最小正周期;
(II)求f(x)在区间[0, ]上的最大值和最小值.
]上的最大值和最小值.
解:∵f(x)=sinxcosx- sin2x
sin2x
= sin2x-
sin2x- •
• …4
…4
= sin2x+
sin2x+ cos2x-
cos2x-
=sin(2x+ )-
)- …6
…6
∴函数f(x)的最小正周期为π…7
(Ⅱ)由(Ⅰ)知:f(x)=sin(2x+ )-
)- ,
,
∵0≤x≤ ,
,
∴ ≤2x+
≤2x+ ≤
≤ ,
,
∴当2x+ =
= ,即x=
,即x= 时,f(x)取得最大值1-
时,f(x)取得最大值1- ;…10
;…10
当2x+ =
= ,即x=
,即x= 时,f(x)取得最小值-
时,f(x)取得最小值- …13
…13
分析:(Ⅰ)将f(x)=sinxcosx- sin2x化为f(x)=sin(2x+
sin2x化为f(x)=sin(2x+ )-
)- ,即可求其最小正周期;
,即可求其最小正周期;
(Ⅱ)由0≤x≤ ,可求得
,可求得 ≤2x+
≤2x+ ≤
≤ ,由正弦函数的性质即可求得f(x)在区间[0.
,由正弦函数的性质即可求得f(x)在区间[0. ]上的最大值和最小值.
]上的最大值和最小值.
点评:本题考查三角函数中的恒等变换应用,着重考查三角变换(降幂公式与辅助角公式)的应用,属于中档题.
 sin2x
sin2x=
 sin2x-
sin2x- •
• …4
…4=
 sin2x+
sin2x+ cos2x-
cos2x-
=sin(2x+
 )-
)- …6
…6∴函数f(x)的最小正周期为π…7
(Ⅱ)由(Ⅰ)知:f(x)=sin(2x+
 )-
)- ,
,∵0≤x≤
 ,
,∴
 ≤2x+
≤2x+ ≤
≤ ,
,∴当2x+
 =
= ,即x=
,即x= 时,f(x)取得最大值1-
时,f(x)取得最大值1- ;…10
;…10当2x+
 =
= ,即x=
,即x= 时,f(x)取得最小值-
时,f(x)取得最小值- …13
…13分析:(Ⅰ)将f(x)=sinxcosx-
 sin2x化为f(x)=sin(2x+
sin2x化为f(x)=sin(2x+ )-
)- ,即可求其最小正周期;
,即可求其最小正周期;(Ⅱ)由0≤x≤
 ,可求得
,可求得 ≤2x+
≤2x+ ≤
≤ ,由正弦函数的性质即可求得f(x)在区间[0.
,由正弦函数的性质即可求得f(x)在区间[0. ]上的最大值和最小值.
]上的最大值和最小值.点评:本题考查三角函数中的恒等变换应用,着重考查三角变换(降幂公式与辅助角公式)的应用,属于中档题.

练习册系列答案
相关题目
 ,f(x)最大值为2
,f(x)最大值为2 上的单增区间.
上的单增区间. ,求函数y=(log2x+1)(log2x-2)的最大值和最小值并求出取得最值时对应的x值.
,求函数y=(log2x+1)(log2x-2)的最大值和最小值并求出取得最值时对应的x值. ,求z.
,求z. 如图,三行三列的方阵中有9个数aij(i=1,2,3),从中任取三 个数,则任意两个数不同行也不同列的概率是
如图,三行三列的方阵中有9个数aij(i=1,2,3),从中任取三 个数,则任意两个数不同行也不同列的概率是