题目内容
15.设m、n是两条不同的直线,α、β是两个不同的平面,下列命题正确的是( )| A. | 若m?α,n?α,且m、n是异面直线,那么n与α相交 | |
| B. | 若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β | |
| C. | 若m?α,n?α,且m∥β,n∥β,则α∥β | |
| D. | 若m∥α,n∥β,且α∥β,则m∥n |
分析 对4个选项分别进行判断,即可得出结论.
解答  解:若m?α,n?α,且m、n是异面直线,那么n与α相交或平行,故A错误;
解:若m?α,n?α,且m、n是异面直线,那么n与α相交或平行,故A错误;
若α∩β=m,n∥m,且n?α,则n∥α,同理由n?β,可得n∥β,
故B正确;
若m?α,n?α,且m∥β,n∥β,当m,n相交时,则α∥β,
但m,n平行时,结论不一定成立,故C错误;
(如图)A1B1∥面AC,BC∥面A1C1,面AC∥面A1C1,
但A1B1与BC不平行,故D错误.
故选B.
点评 本题考查线面位置关系的判定,考查学生分析解决问题的能力,正确运用定理是关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
6.计算:log5100+log50.25的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
3.已知函数f(x)满足f($\frac{1}{x}$)+$\frac{1}{x}$f(-x)=2x(x≠0),则f(-2)=( )
| A. | $-\frac{7}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{7}{2}$ | D. | $-\frac{9}{2}$ |
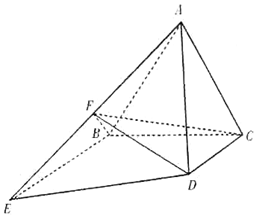 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.