题目内容
(本小题满分12分)已知函数 在同一半周期内的图象过点
在同一半周期内的图象过点 ,其中
,其中 为坐标原点,
为坐标原点, 为函数
为函数 图象的最高点,
图象的最高点, 为函数
为函数 的图象与
的图象与 轴的正半轴的交点.
轴的正半轴的交点.

(Ⅰ)试判断 的形状,并说明理由.
的形状,并说明理由.
(Ⅱ)若将 绕原点
绕原点 按逆时针方向旋转角
按逆时针方向旋转角 时,顶点
时,顶点 恰好同时落在曲线
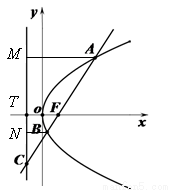
恰好同时落在曲线
 上(如图所示),求实数
上(如图所示),求实数 的值.
的值.
(Ⅰ) 为等边三角形; (Ⅱ)
为等边三角形; (Ⅱ)
【解析】
试题分析:解法一:(Ⅰ) 因为函数 ,所以
,所以 ,所以函数
,所以函数 的半周期为4,
的半周期为4,
所以 . 又因为
. 又因为 为函数
为函数 图象的最高点,所以点
图象的最高点,所以点 坐标为
坐标为 ,所以
,所以 , 又因为
, 又因为 坐标为
坐标为 ,所以
,所以 ,所以
,所以 为等边三角形. (Ⅱ)由(Ⅰ)知,
为等边三角形. (Ⅱ)由(Ⅰ)知, ,所以点
,所以点 ,
, 的坐标分别为
的坐标分别为 ,
, ,代入
,代入 ,得
,得 ,且
,且 , 所以
, 所以 ,即可求出结果.解法二:(Ⅰ)因为函数
,即可求出结果.解法二:(Ⅰ)因为函数 ,所以
,所以 ,所以函数
,所以函数 的半周期为4,所以
的半周期为4,所以 , 因为
, 因为 为函数
为函数 的图象的最高点,所以点
的图象的最高点,所以点 坐标为
坐标为 ,所以
,所以 ,所以
,所以 . 又因为直线
. 又因为直线 的斜率
的斜率 ,所以
,所以 ,所以
,所以 为等边三角形.
为等边三角形.
(Ⅱ)由(Ⅰ)知, ,所以点
,所以点 ,
, 的坐标分别为
的坐标分别为 ,
, ,
,
因为点 ,
, 在函数
在函数 的图象上, 所以
的图象上, 所以 ,可得
,可得 ,所以
,所以 ,进而求出结果.解法三:(Ⅰ)同解法一或同解法二;(Ⅱ)由(Ⅰ)知,
,进而求出结果.解法三:(Ⅰ)同解法一或同解法二;(Ⅱ)由(Ⅰ)知, 为等边三角形.因为函数
为等边三角形.因为函数 的图象关于直线
的图象关于直线 对称, 由图象可知,当
对称, 由图象可知,当 时,点
时,点 ,
, 恰在函数
恰在函数 的图象上. 此时点
的图象上. 此时点 的坐标为
的坐标为 , 所以
, 所以 ,所以所求的实数
,所以所求的实数 的值为4.
的值为4.
试题解析:解法一:(Ⅰ) 为等边三角形. 1分
为等边三角形. 1分
理由如下:
因为函数 ,
,
所以 ,所以函数
,所以函数 的半周期为4,
的半周期为4,
所以 . 2分
. 2分
又因为 为函数
为函数 图象的最高点,
图象的最高点,
所以点 坐标为
坐标为 ,所以
,所以 , 4分
, 4分
又因为 坐标为
坐标为 ,所以
,所以 ,
,
所以 为等边三角形. 6分
为等边三角形. 6分
(Ⅱ)由(Ⅰ)知, ,
,
所以点 ,
, 的坐标分别为
的坐标分别为 ,
, , 7分
, 7分
代入 ,得
,得 ,
,
且 , 9分
, 9分
所以 ,结合
,结合 ,
, ,
,
解得 , 11分
, 11分
所以 ,所以所求的实数
,所以所求的实数 的值为4. 12分
的值为4. 12分
解法二:(Ⅰ) 为等边三角形. 1分
为等边三角形. 1分
理由如下:
因为函数 ,
,
所以 ,所以函数
,所以函数 的半周期为4,所以
的半周期为4,所以 , 2分
, 2分
因为 为函数
为函数 的图象的最高点,
的图象的最高点,
所以点 坐标为
坐标为 ,所以
,所以 ,所以
,所以 . 4分
. 4分
又因为直线 的斜率
的斜率 ,所以
,所以 ,
,
所以 为等边三角形. 6分
为等边三角形. 6分
(Ⅱ)由(Ⅰ)知, ,
,
所以点 ,
, 的坐标分别为
的坐标分别为 ,
, , 7分
, 7分
因为点 ,
, 在函数
在函数 的图象上,
的图象上,
所以 , 8分
, 8分
所以 , 9分
, 9分
消去 得,
得,  ,
,
所以 ,
,
所以 ,所以
,所以 , 10分
, 10分
又因为  ,所以
,所以 ,所以
,所以 , 11分
, 11分
所以 .所以所求的实数
.所以所求的实数 的值为4. 12分
的值为4. 12分
解法三:(Ⅰ)同解法一或同解法二;
(Ⅱ)由(Ⅰ)知, 为等边三角形.
为等边三角形.
因为函数 的图象关于直线
的图象关于直线 对称, 8分
对称, 8分
由图象可知,当 时,点
时,点 ,
, 恰在函数
恰在函数 的图象上. 10分
的图象上. 10分
此时点 的坐标为
的坐标为 , 11分
, 11分
所以 ,所以所求的实数
,所以所求的实数 的值为4. 12分.
的值为4. 12分.
考点:1.三角函数图象与性质;2.数形结合思想.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案 ,
, ,则
,则 ( )
( )



 0.5
0.5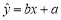 .若
.若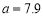 ,则
,则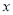 每增加1个单位,
每增加1个单位,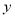 就
就 个单位 B.减少
个单位 B.减少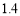 个单位
个单位  个单位 D.减少
个单位 D.减少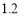 个单位
个单位  的左焦点为
的左焦点为 ,点
,点 是椭圆上异于顶点的任意一点,
是椭圆上异于顶点的任意一点, 为坐标原点.若点
为坐标原点.若点 是线段
是线段 的中点,则
的中点,则 的周长为( ).
的周长为( ). B.
B. C.
C. D.
D.
 轴对称 B.关于
轴对称 B.关于 轴对称
轴对称 对称
对称 ,则
,则 中的所有偶数的和等于 .
中的所有偶数的和等于 .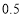 .现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率:先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果.经随机模拟试验产生了如下20组随机数:
.现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率:先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果.经随机模拟试验产生了如下20组随机数: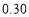 B.
B.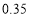 C.
C.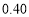 D.
D.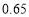

 已知函数
已知函数 ,那么函数y=
,那么函数y= 的大致图象是( )
的大致图象是( )
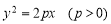 的焦点F的直线
的焦点F的直线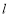 交抛物线于点A、B,交其准线于点C,若
交抛物线于点A、B,交其准线于点C,若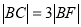 ,且
,且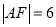 ,则此抛物线的方程为_____________
,则此抛物线的方程为_____________