题目内容
已知向量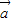
=（ex+
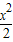，-x），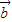
=（1，t），若函数f（x）=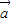
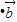在区间（-1，1）上存在增区间，则t 的取值范围为 ．
【答案】分析：先利用数量积的坐标表示求出，f（x）=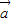
=
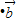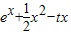，然后对函数求导，由题意可知函数f（x）在（x1，x2）⊆（-1，1）上单调递增，结合函数的单调性与导数的关系即可求解
解答：解：由题意可得，f（x）=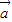
=
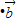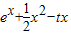
对函数求导可得，f，（x）=ex+x-t
∵函数f（x）在（-1，1）上存在增区间
∴函数f（x）在（x1，x2）⊆（-1，1）上单调递增，
故ex+x＞t在x∈（x1，x2）时时恒成立，
故t＜e+1
故答案为：（-∞，e+1）
点评：本题主要考查了函数的单调性与函数的导数的关系及函数的恒成立问题求解参数的转化的应用
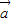
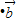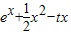=，然后对函数求导，由题意可知函数f（x）在（x1，x2）⊆（-1，1）上单调递增，结合函数的单调性与导数的关系即可求解解答：解：由题意可得，f（x）=
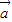
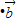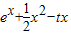
=对函数求导可得，f，（x）=ex+x-t
∵函数f（x）在（-1，1）上存在增区间
∴函数f（x）在（x1，x2）⊆（-1，1）上单调递增，
故ex+x＞t在x∈（x1，x2）时时恒成立，
故t＜e+1
故答案为：（-∞，e+1）
点评：本题主要考查了函数的单调性与函数的导数的关系及函数的恒成立问题求解参数的转化的应用
练习册系列答案
相关题目
= m?n，
且
在x=1处取得极值.
；
图象上，横坐标依次成等差数列，证明：△ABC为钝角三角形，并判断是否可能是等腰三角形，说明理由.