题目内容
已知曲线C上任意一点P到点F(
,0)和直线l:x=
的距离之比为
.
(Ⅰ)求曲线C的方程;
(Ⅱ)设过(0,-2)的直线l与曲线C交于A、B两点,以AB为直径的圆过曲线C的中心,求直线l的方程.
| 3 |
| 4 | ||
|
| ||
| 2 |
(Ⅰ)求曲线C的方程;
(Ⅱ)设过(0,-2)的直线l与曲线C交于A、B两点,以AB为直径的圆过曲线C的中心,求直线l的方程.
考点:轨迹方程,直线的一般式方程,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)直接由题意列式,整理后即可得到曲线C的方程;
(Ⅱ)分类讨论,当直线斜率不存在时不合题意;当直线斜率存在时,写出直线方程,和椭圆方程联立后由根与系数关系得到A,B两点的横纵坐标的积,然后由向量数量积为0得答案.
(Ⅱ)分类讨论,当直线斜率不存在时不合题意;当直线斜率存在时,写出直线方程,和椭圆方程联立后由根与系数关系得到A,B两点的横纵坐标的积,然后由向量数量积为0得答案.
解答:
解:(Ⅰ)设P(x,y),由题意得,
=
,两边平方后整理得:
+y2=1.
故曲线C的方程为:
+y2=1;
(Ⅱ)当直线l的斜率不存在时,不满足题意;
当直线l的斜率存在时,设直线l的方程为y=kx-2,
设A(x1,y1),B(x2,y2),
由方程组
,得(1+4k2)x2-16kx+12=0.
则x1+x2=
,x1x2=
,
∵以AB为直径的圆过曲线C的中心,
∴
⊥
,
∴x1x2+y1y2=0,
∵y1=kx1-2,y2=kx2-2,
y1y2=k2x1x2-2k(x1+x2)+4,
∴(1+k2)x1x2-2k(x1+x2)+4=0,
∴(1+k2)•
-2k•
+4=0,
解得:k=2或k=-2,
经检验符合△>0.
∴直线l的方程为:y=2x-2或y=-2x-2.
| ||||
|x-
|
| ||
| 2 |
| x2 |
| 4 |
故曲线C的方程为:
| x2 |
| 4 |
(Ⅱ)当直线l的斜率不存在时,不满足题意;
当直线l的斜率存在时,设直线l的方程为y=kx-2,
设A(x1,y1),B(x2,y2),
由方程组
|
则x1+x2=
| 16k |
| 1+4k2 |
| 12 |
| 1+4k2 |
∵以AB为直径的圆过曲线C的中心,
∴
| OA |
| OB |
∴x1x2+y1y2=0,
∵y1=kx1-2,y2=kx2-2,
y1y2=k2x1x2-2k(x1+x2)+4,
∴(1+k2)x1x2-2k(x1+x2)+4=0,
∴(1+k2)•
| 12 |
| 1+4k2 |
| 16k |
| 1+4k2 |
解得:k=2或k=-2,
经检验符合△>0.
∴直线l的方程为:y=2x-2或y=-2x-2.
点评:本题考查了轨迹方程的求法,考查了直线与圆锥曲线的关系,涉及直线与圆锥曲线关系问题,常采用联立直线方程与圆锥曲线方程,然后利用根与系数关系求解,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
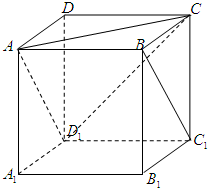 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: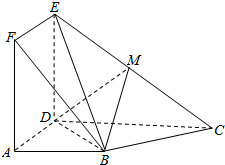 正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=