题目内容
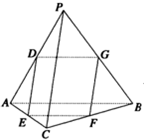如图，在四面体P-ABC中，PC⊥AB，PA⊥BC，点D、E、F、G分别是棱AP、AC、CB、BP的中点；
（1）求证：DE∥平面BCP；
（2）求证：四边形DEFG为矩形．
证明：（1）∵D、E、F、G分别是棱AP、AC、CB、BP的中点
∴DE
PC，GFPC
∴DEGF
∵DE?平面BCP，GF⊆平面BCP
∴DE∥平面BCP
（2）由（1）可得DEGF，DGEF
∴四边形DEFG为平行四边形
∵PC⊥AB，DEPC，DGAB
∴DE⊥DG
∴四边形DEFG为矩形
分析：（1）要证DE∥平面BCP根据线面平行的判定定理需证明DE与平面BCP内的一条直线平行而者可通过D、E、F、G分别是棱AP、AC、CB、BP的中点利用中位线定理和平行的传递性即可得出DEGF．
（2）根据（1）可得DEGF即四边形DEFG为平行四边形再利用PC⊥AB和中位线定理可得DE⊥DG故四边形DEFG为矩形．
点评：本题主要考察线面平行的判定和矩形的证明，属常考题，较难．解题的关键是透彻理解线面平行的判定定理和平面四边形为矩形的判定定理，同时要注意中位线定理在本题中的应用！
∴DE
PC，GFPC∴DE
GF∵DE?平面BCP，GF⊆平面BCP
∴DE∥平面BCP
（2）由（1）可得DE
GF，DGEF∴四边形DEFG为平行四边形
∵PC⊥AB，DE
PC，DGAB∴DE⊥DG
∴四边形DEFG为矩形
分析：（1）要证DE∥平面BCP根据线面平行的判定定理需证明DE与平面BCP内的一条直线平行而者可通过D、E、F、G分别是棱AP、AC、CB、BP的中点利用中位线定理和平行的传递性即可得出DE
GF．（2）根据（1）可得DE
GF即四边形DEFG为平行四边形再利用PC⊥AB和中位线定理可得DE⊥DG故四边形DEFG为矩形．点评：本题主要考察线面平行的判定和矩形的证明，属常考题，较难．解题的关键是透彻理解线面平行的判定定理和平面四边形为矩形的判定定理，同时要注意中位线定理在本题中的应用！
练习册系列答案
习题精选系列答案
相关题目
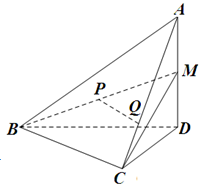（2013•浙江）如图，在四面体A-BCD中，AD⊥平面BCD，
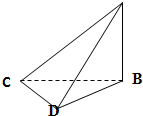给出以下判断：
．M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ=3QC．
B.
C.-
D.