题目内容
 给出以下判断:
给出以下判断:(1)b=0是函数f(x)=ax2+bx+c为偶函数的充要条件;
(2)椭圆
| x2 |
| 4 |
| y2 |
| 3 |
(3)回归直线
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
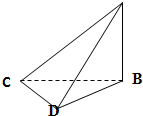
(4)如图,在四面体ABCD中,设E为△BCD的重心,则
| AE |
| AB |
| 1 |
| 2 |
| AC |
| 2 |
| 3 |
| AD |
(5)双曲线
| x2 |
| a2 |
| y2 |
| b2 |
分析:(1)利用充要条件的判断方法判断;
(2)利用点差法,求出以点(1,1)为中点的弦所在直线方程;
(3)回归直线
=
x+
必过点(
,
),故正确;
(4)利用向量的线性运算可得结论;
(5)设△PF1F2的内切圆分别与PF1、PF2切于点A、B,与F1F2切于点M,则|PA|=|PB|,|F1A|=|F1M|,|F2B|=|F2M|,又点P在双曲线右支上⇒|PF1|-|PF2|=2a⇒|F1M|-|F2M|=2a.而|F1M|+|F2M|=2c,设M点坐标为(x,0),则由|F1M|-|F2M|=2a,⇒(x+c)-(c-x)=2a,可解得x=a,显然内切圆的圆心与点M的连线垂直于x轴,于是问题解决.
(2)利用点差法,求出以点(1,1)为中点的弦所在直线方程;
(3)回归直线
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
(4)利用向量的线性运算可得结论;
(5)设△PF1F2的内切圆分别与PF1、PF2切于点A、B,与F1F2切于点M,则|PA|=|PB|,|F1A|=|F1M|,|F2B|=|F2M|,又点P在双曲线右支上⇒|PF1|-|PF2|=2a⇒|F1M|-|F2M|=2a.而|F1M|+|F2M|=2c,设M点坐标为(x,0),则由|F1M|-|F2M|=2a,⇒(x+c)-(c-x)=2a,可解得x=a,显然内切圆的圆心与点M的连线垂直于x轴,于是问题解决.
解答:解:(1)函数f(x)=ax2+bx+c是偶函数,可得f(-x)=f(x),得a(-x)2-bx+c=ax2+bx+c,∴-bx=bx,∴b=0;当b=0时,f(x)=ax2+c,满足f(-x)=f(x),是偶函数,所以b=0是函数f(x)=ax2+bx+c为偶函数的充要条件,故(1)正确;
(2)设以A(1,1)为中点椭圆的弦与椭圆交于E(x1,y1),F(x2,y2),∵A(1,1)为EF中点,∴x1+x2=2,y1+y2=2,把E(x1,y1),F(x2,y2)分别代入椭圆
+
=1,得
,∴3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,∴6(x1-x2)+8(y1-y2)=0,∴k=
=-
,∴以A(1,1)为中点椭圆的弦所在的直线方程为3x+4y-7=0,故(2)错误;
(3)回归直线
=
x+
必过点(
,
),故正确;
(4)在四面体ABCD中,设E为△BCD的重心,则
=
+
=
+
•
(
+
)=
(
+
+
),故(4)不正确;
(5)设△PF1F2的内切圆分别与PF1、PF2切于点A、B,与F1F2切于点M,则|PA|=|PB|,|F1A|=|F1M|,|F2B|=|F2M|.又点P在双曲线右支上,∴|PF1|-|PF2|=2a,即(|PA|+|F1A|)-(|PB|+|F2B|)=2a,∴|F1M|-|F2M|=2a,而|F1M|+|F2M|=2c,设M点坐标为(x,0),∵|F1M|-|F2M|=2a,∴(x+c)-(c-x)=2a,解得x=a,故(5)正确.
故答案为:(1)(3)(5).
(2)设以A(1,1)为中点椭圆的弦与椭圆交于E(x1,y1),F(x2,y2),∵A(1,1)为EF中点,∴x1+x2=2,y1+y2=2,把E(x1,y1),F(x2,y2)分别代入椭圆
| x2 |
| 4 |
| y2 |
| 3 |
|
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
(3)回归直线
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
(4)在四面体ABCD中,设E为△BCD的重心,则
| AE |
| AB |
| BE |
| AB |
| 2 |
| 3 |
| 1 |
| 2 |
| BC |
| BD |
| 1 |
| 3 |
| AB |
| AC |
| AD |
(5)设△PF1F2的内切圆分别与PF1、PF2切于点A、B,与F1F2切于点M,则|PA|=|PB|,|F1A|=|F1M|,|F2B|=|F2M|.又点P在双曲线右支上,∴|PF1|-|PF2|=2a,即(|PA|+|F1A|)-(|PB|+|F2B|)=2a,∴|F1M|-|F2M|=2a,而|F1M|+|F2M|=2c,设M点坐标为(x,0),∵|F1M|-|F2M|=2a,∴(x+c)-(c-x)=2a,解得x=a,故(5)正确.
故答案为:(1)(3)(5).
点评:本题考查命题真假的判断,涉及的知识点多,需要逐个判断,有难度.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
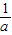 ,则a>1; ②若0<α<π,0<β<
,则a>1; ②若0<α<π,0<β<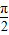 ,则α-β∈(0,
,则α-β∈(0,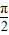 ); ③若|a|>|b|,则a2>b2;
); ③若|a|>|b|,则a2>b2;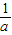 <
<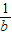 ; ⑤若ac2>bc2,则a>b; ⑥若a>b,c>d,则
; ⑤若ac2>bc2,则a>b; ⑥若a>b,c>d,则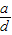 >
>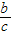 .
.