题目内容
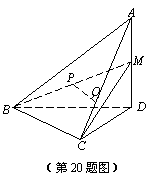
如图,在四面体A−BCD中,AD^平面BCD,BC^CD,AD=2,BD=2![]() .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
(Ⅰ)证明:PQ∥平面BCD;
(Ⅱ)若二面角C−BM−D的大小为60°,求ÐBDC的大小.
【命题意图】本题考查空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同时考查空间想象能力和运算求解能力。
【答案解析】
(Ⅰ)取BD的中点O,在线段CD上取点F,使得DF=3FC,连接OP,OF,FQ.
因为AQ=3QC,所以
QF∥AD,且QF=![]() AD
AD
因为O,P分别为BD,BM的中点,所以OP是△BDM的中位线,所以
OP∥DM,且OP=![]() DM
DM
又点M是AD的中点,所以
OP∥AD,且OP=![]() AD
AD
从而
OP∥FQ,且OP=FQ
所以四边形OPQF是平行四边形,故
PQ∥OF
又PQË平面BCD,OFÌ平面BCD,所以
PQ∥平面BCD.
(Ⅱ)作CG^BD于点G,作GH^BM于点HG,连接CH,则CH^BM,所以ÐCHG为二面角的平面角。设ÐBDC=θ.
在Rt△BCD中,
CD=BDcos θ=2![]() cos θ,
cos θ,
CG=CDsin θ=2![]() cos θsin θ,
cos θsin θ,
BG=BCsin θ=2![]() sin2θ
sin2θ
在Rt△BDM中,
HG=![]() =
=![]()
在Rt△CHG中,
tanÐCHG=![]()
所以
tan q=![]()
从而
q=60°
即ÐBDC=60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2009•武汉模拟)如图,在四面体A-BCD中,
(2009•武汉模拟)如图,在四面体A-BCD中, (2013•浙江)如图,在四面体A-BCD中,AD⊥平面BCD,
(2013•浙江)如图,在四面体A-BCD中,AD⊥平面BCD,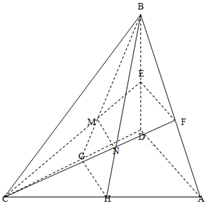 如图,在四面体A-BCD中,有CB=CD,平面ABD⊥平面BCD,点E、F分别为BD,AB的中点,MN∥平面ABD.
如图,在四面体A-BCD中,有CB=CD,平面ABD⊥平面BCD,点E、F分别为BD,AB的中点,MN∥平面ABD.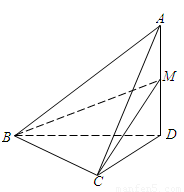
 平面ADC;
平面ADC;