题目内容
9．将下列角度化为弧度，弧度转化为角度（1）780°，（2）-1560°，（3）67.5°（4）$-\frac{10}{3}π$，（5）$\frac{π}{12}$，（6）$\frac{7π}{4}$．
分析 利用π弧度=180°即可得出．
解答 解：（1）780°=$\frac{780}{180}×π$弧度=$\frac{13π}{3}$弧度，
（2）-1560°=-$\frac{1560}{180}×π$弧度=-$\frac{26}{3}$π弧度，
（3）67.5°=$\frac{67.5}{180}π$弧度=$\frac{3π}{8}$弧度．
（4）$-\frac{10}{3}π$弧度=-$\frac{10}{3}×18{0}^{°}$=-600°，
（5）$\frac{π}{12}$弧度=$\frac{18{0}^{°}}{12}$=15°，
（6）$\frac{7π}{4}$弧度=$\frac{7}{4}×18{0}^{°}$=315°．
点评 本题考查了弧度与角度的换算关系，考查了推理能力与计算能力，属于基础题．
练习册系列答案
考前必练系列答案
相关题目
15．
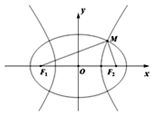已知椭圆C1：$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1（m＞p＞0）与双曲线C2：$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1（n＞0）有公共的焦点F1，F2，设M为C1与C2在第一象限内的交点，|F1F2|=2c．则（ ）
已知椭圆C1：$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1（m＞p＞0）与双曲线C2：$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1（n＞0）有公共的焦点F1，F2，设M为C1与C2在第一象限内的交点，|F1F2|=2c．则（ ）| A． | m2+n2=2c2，且∠F1MF2＞$\frac{π}{2}$ | B． | m2+n2=2c2，且∠F1MF2=$\frac{π}{2}$ | ||
| C． | m2+n2=4c2，且∠F1MF2＞$\frac{π}{2}$ | D． | m2+n2=4c2，且∠F1MF2=$\frac{π}{2}$ |
13．2017年春晚过后，为了研究演员上春晚次数与受关注度的关系，某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计，得到如下数据：
（1）若该演员的粉丝数量g（x）≤g（1）=0与上春晚次数x满足线性回归方程，试求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并就此分析，该演员上春晚12次时的粉丝数量；
（2）若用$\frac{{y}_{i}}{{x}_{i}}$（i=1，2，3，4，5）表示统计数据时粉丝的“即时均值”（四舍五入，精确到整数），从这5个“即时均值”中任选2数，记所选的2数之和为随机变量η，求η的分布列与数学期望．
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
| 上春晚次数x（单位：次） | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y（单位：万人） | 10 | 20 | 40 | 80 | 100 |
（2）若用$\frac{{y}_{i}}{{x}_{i}}$（i=1，2，3，4，5）表示统计数据时粉丝的“即时均值”（四舍五入，精确到整数），从这5个“即时均值”中任选2数，记所选的2数之和为随机变量η，求η的分布列与数学期望．
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
18．下表是某位理科学生连续5次月考的物理、数学的成绩，结果如下：
（Ⅰ）求该生5次月考物理成绩的平均分和方差；
（Ⅱ）一般来说，学生的数学成绩与物理成绩有较强的线性相关关系，根据上表提供的数据，求两个变量x，y的线性回归方程．（小数点后保留一位有效数字）
参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$，$\overline{x}$，$\overline{y}$表示样本均值
参考数据：902+852+742+682+632=29394，
90×130×85×125×74×110×68×95+63×90=42595．
| 次数 | 1 | 2 | 3 | 4 | 5 |
| 物理（x分） | 90 | 85 | 74 | 68 | 63 |
| 数学（y分） | 130 | 125 | 110 | 95 | 90 |
（Ⅱ）一般来说，学生的数学成绩与物理成绩有较强的线性相关关系，根据上表提供的数据，求两个变量x，y的线性回归方程．（小数点后保留一位有效数字）
参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$，$\overline{x}$，$\overline{y}$表示样本均值
参考数据：902+852+742+682+632=29394，
90×130×85×125×74×110×68×95+63×90=42595．
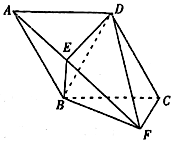如图，平面ABCD⊥平面BCF，四边形ABCD是菱形，∠BCF=90°．