题目内容
如图所示，A、B为函数
图象上两点，且AB∥
轴，点M（1，m）（m>3）是△ABC边AC的中点。
（1）设点B的横坐标为t，△ABC的面积为S，求S关于t的函数关系式S=
；
（2）求函数S=的最大值，并求出相应的点C的坐标。
解：（1）设
点M是△ABC边AC的中点，则
（2）设
，因为M是△ABC边AC的中点，
，
① 当
时,令
得
,
在区间(0,
)上,
, S=
递增；在区间(，1 ]上,
, S=递减；
∴时，函数S=取最大值，最大值是
.
此时点C的坐标为
.
② 当m>9时, >0, S=是(0,1]增函数,
∴当t=1时, 函数S=取最大值
,此时点C的坐标为
.
练习册系列答案
相关题目
已知函数f（x）的定义域为[-3，+∞），部分函数值如表所示，其导函数的图象如图所示，若正数a，b满足f（2a+b）＜1，则
的取值范围是（ ）
| b+2 |
| a+2 |
A、(
| ||
B、(
| ||
| C、（1，4） | ||
D、(-∞，
|
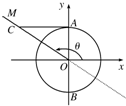如图所示，已知单位圆O与y轴交于A、B两点，角θ的顶点为原点，始边在x轴的非负半轴上，终边在射线OM上，过点A作直线AC垂直于y轴与角θ的终边OM交于点C，则有向线段AC表示的函数值是什么？
已知函数f（x）的定义域为[-2，+∞），部分函数值如下表，f'（x）为f（x）的导函数，f'（x）的图象如图所示．如果实数a满足f（a）＜1，则a的取值范围是（ ）
已知函数f（x）的定义域为[-3，+∞），部分函数值如表所示，其导函数的图象如图所示，若正数a，b满足f（2a+b）＜1，则
在定义域(－
，3)内可导，其图象如图所示，记
，则不等式
的解集为( )
，1]∪[2,3)
B．[－1，
]∪[
，
]