题目内容
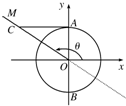 如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?
如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?分析:直角三角形OAC中,利用边角关系可得tan∠AOC=
=-cotθ,再由有向线段AC=-|AC|,可得 cotθ=-
=AC,从而得出结论.
| |AC| |
| |OA| |
| |AC| |
| |OA| |
解答:解:直角三角形OAC中,利用边角关系可得tan∠AOC=
=tan(θ-
)=-cotθ,
再由AC=-|AC|,可得 cotθ=-
=-
=AC,故有向线段AC表示的函数值是cotθ=
.
| |AC| |
| |OA| |
| π |
| 2 |
再由AC=-|AC|,可得 cotθ=-
| |AC| |
| |OA| |
| -AC |
| 1 |
| 1 |
| tanθ |
点评:本题主要考查任意角的三角函数的定义、诱导公式,以及直角三角形中的边角关系,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
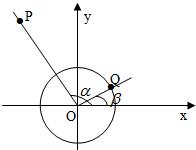 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
