题目内容
5．已知f（x）的定义域为实数集R，?x∈R，f（3+2x）=f（7-2x），若f（x）=0恰有n个不同实数根，且这n个不同实数根之和等于75，则n=15．分析 由条件可得f（x）=f（10-x），即图象关于x=5对称，可得f（x）=0n个不同实数根每两个根的和为10，只需求出共有几组10即可．
解答 解：?x∈R，f（3+2x）=f（7-2x），
∴令t=3+2x，2x=t-3．
∴f（t）=f（10-t）\
∴f（x）=f（10-x）
∵f（5）=0，
∵（75-5）÷10=7，
∴n=2×7+1=15．
故答案为15．
点评 考查了抽象函数的对称性和利用对称性解决实际问题．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
20．已知二次函数f（x）=ax2+bx+c（a≠0），若关于x的不等式f（x）＞0的解集为{x|x＜-2或x＞4}，则下列结论正确的是（ ）
| A． | a＞0，-$\frac{b}{2a}$=1 | B． | a＜0，$\frac{c}{a}$=-8 | C． | a＜0，-$\frac{b}{2a}$=-1 | D． | a＞0，$\frac{c}{a}$=8 |
17．已知函数f（x）=Asin（ωx+φ）（A，ω，φ均为正的常数）的最小正周期为π，当x=$\frac{2π}{3}$时，函数f（x）取得最小值，则下列结论正确的是（ ）
| A． | f（1）＜f（-1）＜f（0） | B． | f（0）＜f（1）＜f（-1） | C． | f（-1）＜f（0）＜f（1） | D． | f（1）＜f（0）＜f（-1） |
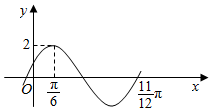函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示．