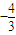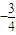题目内容
已知△ABC中,2sinAcosB=sinCcosB+cosCsinB,
(Ⅰ)求角B的大小;
(Ⅱ)设向量m=(cosA,cos2A),n=(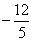 ,1),求当m·n取最小值时,
,1),求当m·n取最小值时,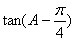 的值。
的值。
(Ⅰ)求角B的大小;
(Ⅱ)设向量m=(cosA,cos2A),n=(
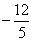 ,1),求当m·n取最小值时,
,1),求当m·n取最小值时,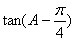 的值。
的值。 解:(Ⅰ)因为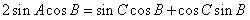 ,
,
所以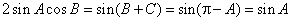 ,
,
因为0<A<π,所以sinA≠0,
所以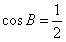 ,
,
因为0<B<π,所以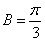 ;
;
(Ⅱ)因为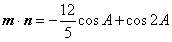 ,
,
所以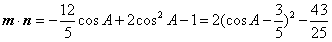 ,
,
所以当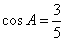 时,m·n取得最小值,
时,m·n取得最小值,
此时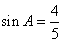 (0<A<π),
(0<A<π),
于是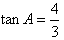 ,
,
所以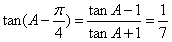 。
。
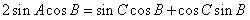 ,
,所以
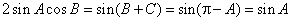 ,
,因为0<A<π,所以sinA≠0,
所以
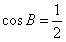 ,
,因为0<B<π,所以
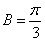 ;
;(Ⅱ)因为
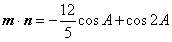 ,
,所以
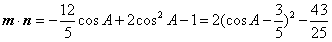 ,
,所以当
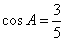 时,m·n取得最小值,
时,m·n取得最小值,此时
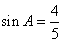 (0<A<π),
(0<A<π),于是
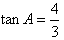 ,
,所以
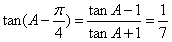 。
。
练习册系列答案
相关题目