题目内容
已知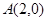 ,
,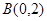 ,
,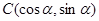 ,
,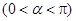 .
.
(1)若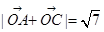 (
(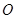 为坐标原点),求
为坐标原点),求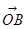 与
与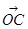 的夹角;
的夹角;
(2)若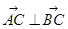 ,求
,求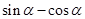 的值.
的值.
(1)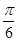 ;(2)
;(2)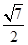
解析试题分析:(1)∵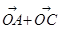 =(2+cosα,sinα),(
=(2+cosα,sinα),(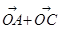 )2=7,∴(2+cosα)2+sin2α=7,∴cosα=
)2=7,∴(2+cosα)2+sin2α=7,∴cosα= . 又B(0,2),C(cosα,sinα),设
. 又B(0,2),C(cosα,sinα),设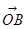 与
与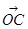 的夹角为θ,则cosθ=
的夹角为θ,则cosθ=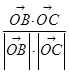 =sinα=±
=sinα=±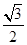 ,∴
,∴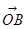 与
与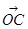 的夹角为
的夹角为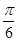 或
或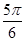 ,又
,又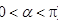 ,∴
,∴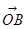 与
与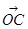 的夹角为
的夹角为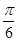 ;
;
(2)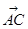 =(cosα-2,sinα),
=(cosα-2,sinα),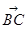 =(cosα,sinα-2),由
=(cosα,sinα-2),由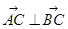 ,∴
,∴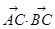 =0,可得cosα+sinα=
=0,可得cosα+sinα= ,∴(cosα+sinα)2=
,∴(cosα+sinα)2=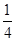 ,∴2sinαcosα=-
,∴2sinαcosα=-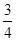 ,∵α∈(0,π),∴α∈(
,∵α∈(0,π),∴α∈( ,π),又由(sinα-cosα)2=1-2sinαcosα=
,π),又由(sinα-cosα)2=1-2sinαcosα=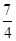 ,sinα-cosα>0,∴sinα-cosα=
,sinα-cosα>0,∴sinα-cosα=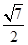
考点:本题考查了三角函数与向量的数量积的关系
点评:此类问题常常由数量积的知识找到三角函数间的关系,再化简所给三角函数式就可得到

练习册系列答案
相关题目