题目内容
给出下列命题:
①“数列{an}为等比数列”是“数列{anan+1}为等比数列”的充分不必要条件;
②“a=2”是“函数f(x)=|x-a|在区间[2,+∞)上为增函数”的充要条件;
③“m=3”是“直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直”的充要条件;
④设a,b,c分别是△ABC三个内角A,B,C所对的边,若a=1,b=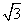 ,则“A=30°”是“B=60°”的必要不充分条件.
,则“A=30°”是“B=60°”的必要不充分条件.
其中,真命题的序号是________.
①④
解析 对于①,当数列{an}是等比数列时,易知数列{anan+1}是等比数列;但当数列{anan+1}是等比数列时,数列{an}未必是等比数列,如数列1,3,2,6,4,12,8显然不是等比数列,而相应的数列3,6,12,24,48,96是等比数列,因此①正确.对于②,当a≤2时,函数f(x)=|x-a|在区间[2,+∞)上是增函数,因此②不正确.对于③,当m=3时,相应的两条直线垂直;反过来,当这两条直线垂直时,不一定能得出m=3,也可能得出m=0,因此③不正确.对于④,由题意,得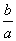 =
=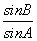 =
=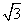 ,当B=60°时,有sin A=
,当B=60°时,有sin A= ,注意到b>a,故A=30°;但当A=30°时,有sin B=
,注意到b>a,故A=30°;但当A=30°时,有sin B=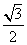 ,B=60°或B=120°,因此④正确.
,B=60°或B=120°,因此④正确.

练习册系列答案
相关题目
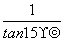 等于( )
等于( )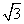 C.4 D.
C.4 D.
 ,且a+b+c=1 (其中a,b,c为正实数),则M的取值范围是( )
,且a+b+c=1 (其中a,b,c为正实数),则M的取值范围是( ) C.[1,8) D.[8,+∞)
C.[1,8) D.[8,+∞)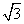 bc,
bc,