Question

（14分）已知长方体ABCD—A₁B₁C₁D₁中, A₁A=AB，

E、F分别是BD₁和AD中点.

       （1）求异面直线CD₁、EF所成的角；

       （2）证明EF是异面直线AD和BD₁的公垂线.

                                          

Answer 1

（1）解：∵在平行四边形中，E也是的中点，∴，（2分）

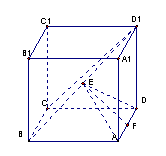∴两相交直线D₁C与CD₁所成的角即异面直线CD₁与EF所成的角.（4分）又A₁A=AB，长方体的侧面都是正方形，∴D₁CCD₁

∴异面直线CD₁、EF所成的角为90°.（7分）

（2）证：设AB=AA₁=a, ∵D₁F=∴EF⊥BD₁（9分）

由平行四边形，知E也是的中点，且点E是长方体ABCD—A₁B₁C₁D₁的对称中心，（12分）∴EA=ED，∴EF⊥AD，又EF⊥BD₁，∴EF是异面直线BD₁与AD的公垂线.（14分）