Question

已知长方体ABCD-A₁B₁C₁D₁中，M、N分别是BB₁和BC的中点，AB=4，AD=2，BB1=2

15

，求异面直线B₁D与MN所成角的余弦值．

Answer 1

分析：连结B₁C，利用三角形中位线的性质得到MN∥B₁C，然后通过解直角三角形求出三角形DB₁C的三边，最后利用余弦定理求异面直线B₁D与MN所成角的余弦值．

解答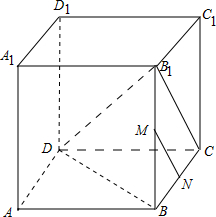：解：如图：
连结B₁C，因为M，N分别为BB₁和BC的中点，所以MN∥B₁C，
则∠DB₁C为异面直线B₁D与MN所成角．
在直角三角形B₁C₁C中，B1C=

B1C12+CC12

=

22+(2 15 )2

=8．
连结BD，则BD=

42+22

=2

5

，在直角三角形B₁BD中，B1D=

BD2+BB12

=

(2 5 )2+(2 15 )2

=4

5

．
在三角形DB₁C中，cos∠DB1C=

B1D2+B1C2-DC2

2B1D•B1C

=

(4 5 )2+82-42

2×4 5 ×8

=

2 5

5

．
所以异面直线B₁D与MN所成角的余弦值为

2 5

5

．

点评：本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力．在立体几何中找平行线是解决问题的一个重要技巧，这个技巧就是通过三角形的中位线找平行线，如果试题的已知中涉及到多个中点，则找中点是出现平行线的关键技巧．