题目内容
已知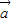 =(cos
=(cos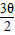 ,sin
,sin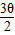 ),
),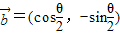 ,且
,且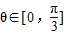
(I)求
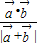 的最值;
的最值;(II)是否存在k的值使
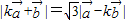 ?
?
【答案】分析:(I)由数量积的定义可得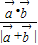 =cosθ-
=cosθ-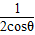 ,下面换元后由函数的最值可得;
,下面换元后由函数的最值可得;
(II)假设存在k的值满足题设,即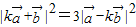 ,然后由三角函数的值域解关于k的不等式组可得k的范围.
,然后由三角函数的值域解关于k的不等式组可得k的范围.
解答:解:(I)由已知得: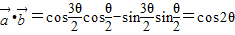
∴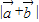 =
=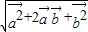 =2cosθ
=2cosθ
∴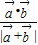 =
=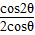 =cosθ-
=cosθ-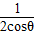
令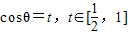
∴cosθ-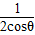 =t-
=t-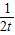 ,(t-
,(t-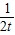 )′=1+
)′=1+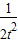 >0
>0
∴t-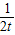 为增函数,其最大值为
为增函数,其最大值为 ,最小值为-
,最小值为-
∴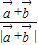 的最大值为
的最大值为 ,最小值为-
,最小值为-
(II)假设存在k的值满足题设,即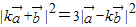
∵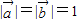 ,
,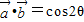
∴cos2θ=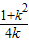
∵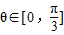 ,∴
,∴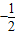 ≤cos2θ≤1
≤cos2θ≤1
∴-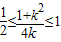
∴0<k≤2+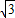
故存在k的值使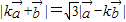
点评:本题为向量的综合应用,涉及向量的模长和导数法求最值,属中档题.
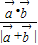 =cosθ-
=cosθ-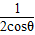 ,下面换元后由函数的最值可得;
,下面换元后由函数的最值可得;(II)假设存在k的值满足题设,即
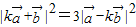 ,然后由三角函数的值域解关于k的不等式组可得k的范围.
,然后由三角函数的值域解关于k的不等式组可得k的范围.解答:解:(I)由已知得:
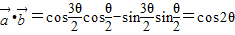
∴
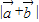 =
=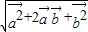 =2cosθ
=2cosθ∴
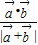 =
=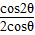 =cosθ-
=cosθ-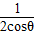
令
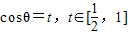
∴cosθ-
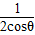 =t-
=t-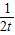 ,(t-
,(t-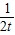 )′=1+
)′=1+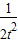 >0
>0∴t-
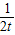 为增函数,其最大值为
为增函数,其最大值为 ,最小值为-
,最小值为-
∴
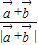 的最大值为
的最大值为 ,最小值为-
,最小值为-
(II)假设存在k的值满足题设,即
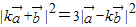
∵
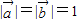 ,
,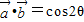
∴cos2θ=
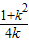
∵
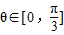 ,∴
,∴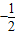 ≤cos2θ≤1
≤cos2θ≤1 ∴-
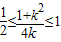
∴0<k≤2+
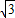
故存在k的值使
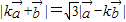
点评:本题为向量的综合应用,涉及向量的模长和导数法求最值,属中档题.

练习册系列答案
相关题目