题目内容
(本题满分14分)已知数列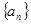 的前
的前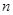 项和为
项和为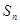 ,且
,且 .
.
(Ⅰ)求数列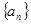 的通项公式;
的通项公式;
(Ⅱ)若数列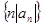 的前
的前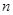 项和为
项和为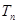 ,求数列
,求数列 的通项公式.
的通项公式.
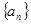 的前
的前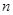 项和为
项和为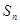 ,且
,且 .
.(Ⅰ)求数列
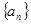 的通项公式;
的通项公式;(Ⅱ)若数列
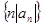 的前
的前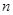 项和为
项和为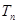 ,求数列
,求数列 的通项公式.
的通项公式.(1)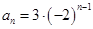 ,
,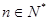 ;(2)
;(2)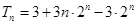 .
.
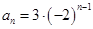 ,
,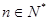 ;(2)
;(2)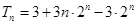 .
.第一问利用数列的前n项和与通项公式的关系可知,
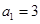 ,当
,当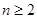 时,
时,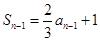 ,
,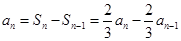
然后利用递推关系式得到通项公式
第二问中,利用第一问的结论,可知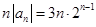 ,然后利用错位相减法得到结论。
,然后利用错位相减法得到结论。
解:(Ⅰ)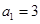 ,当
,当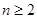 时,
时,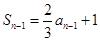 ,
,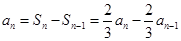 ,
,
∴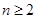 时,
时,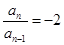 ∴数列
∴数列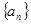 是首项为
是首项为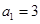 ,公比为
,公比为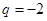 的等比数列,
的等比数列,
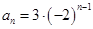 ,
,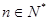 ……………………………………………………………7分
……………………………………………………………7分
(Ⅱ)由(Ⅰ)知,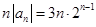
∴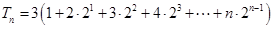
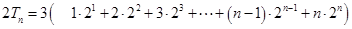
∴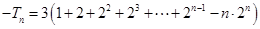
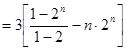
∴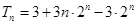 ……………………………………………………………14分
……………………………………………………………14分
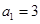 ,当
,当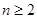 时,
时,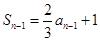 ,
,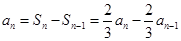
然后利用递推关系式得到通项公式
第二问中,利用第一问的结论,可知
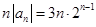 ,然后利用错位相减法得到结论。
,然后利用错位相减法得到结论。解:(Ⅰ)
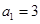 ,当
,当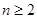 时,
时,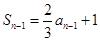 ,
,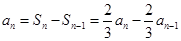 ,
,∴
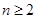 时,
时,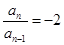 ∴数列
∴数列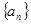 是首项为
是首项为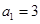 ,公比为
,公比为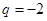 的等比数列,
的等比数列,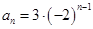 ,
,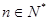 ……………………………………………………………7分
……………………………………………………………7分(Ⅱ)由(Ⅰ)知,
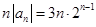
∴
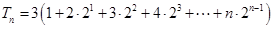
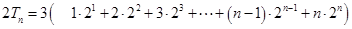
∴
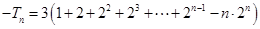
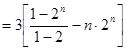
∴
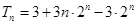 ……………………………………………………………14分
……………………………………………………………14分
练习册系列答案
相关题目
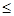 xn<xn+1<3;
xn<xn+1<3;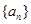 中,
中,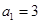 ,前
,前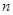 项和为
项和为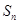 ,等比数列
,等比数列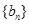 各项均为正数,
各项均为正数,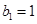 ,且
,且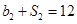 ,
,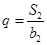
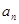 与
与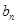 ;
;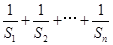
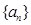 满足
满足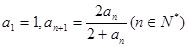 ,
,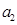 、
、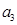 、
、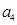 ;
;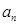 ,并用数学归纳法进行证明
,并用数学归纳法进行证明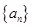 是等差数列,
是等差数列,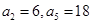 ;数列
;数列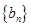 的前n项和是
的前n项和是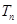 ,且
,且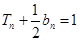 .
.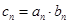 ,求
,求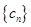 的前n项和
的前n项和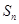
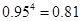 ,
,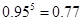 ,
, ,
,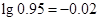 )
)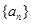 (公差不为零)和等差数列
(公差不为零)和等差数列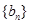 ,如果关于
,如果关于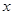 的方程
的方程 有解,那么以下九个方程已知等差数列
有解,那么以下九个方程已知等差数列 ,
, 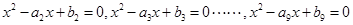 中,
中,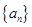 的前
的前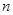 项和为
项和为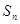 ,等比数列
,等比数列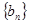 的前
的前 已知数列
已知数列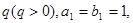

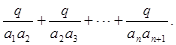
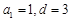 确定的等差数列
确定的等差数列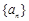 ,当
,当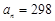 时序号
时序号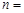 ( )
( )