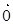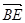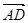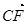题目内容
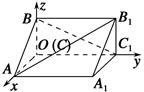
如图,在空间直角坐标系中有直三棱柱ABCA1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( ).

A.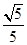 | B.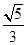 | C.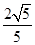 | D.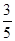 |
A
设CA=2,则C(0,0,0),A(2,0,0),B(0,0,1),C1(0,2,0),B1(0,2,1),可得 =(-2,2,1),
=(-2,2,1), =(0,2,-1),由向量的夹角公式得cos〈
=(0,2,-1),由向量的夹角公式得cos〈 ,
, 〉=
〉=
 =(-2,2,1),
=(-2,2,1), =(0,2,-1),由向量的夹角公式得cos〈
=(0,2,-1),由向量的夹角公式得cos〈 ,
, 〉=
〉=

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
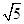 ,AB=AD=
,AB=AD=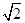 .将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
.将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).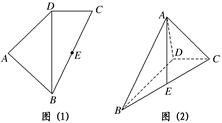
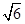 ,M是CC1的中点.
,M是CC1的中点.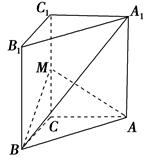
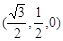 ,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
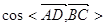 的值.
的值.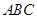 的底边
的底边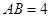 ,点
,点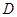 在线段
在线段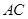 上,
上,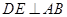 于
于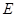 ,现将
,现将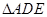 沿
沿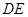 折起到
折起到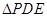 的位置(如图(2)).
的位置(如图(2)).
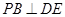 ;
;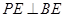 ,直线
,直线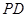 与平面
与平面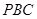 所成的角为
所成的角为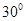 ,求
,求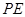 长.
长.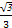
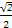


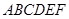 中,
中,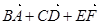
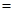 ( )
( )